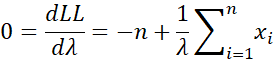Basic Concepts
The Poisson distribution is characterized by the λ parameter which is the mean of the distribution. We can use the mean of a sample, x1, .., xn (taking non-negative integer values only) as an estimate of the lambda parameter.
The log-likelihood function is
For those of you familiar with calculus, we can find the value of lambda that maximizes LL by setting the derivative of LL to zero.
Thus
Thus, the sample mean is the MoM and MLE estimate of lambda.
Note that when λ = x̄
Example
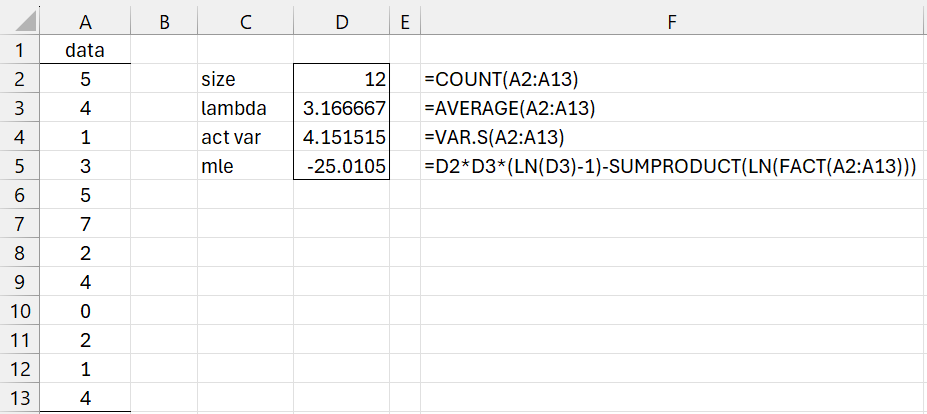
Example 1: Estimate the lambda parameter for the data in column A of Figure 1.
The result is shown on the right side of the figure.
Figure 1 – Fitting a Poisson Distribution
Note that the variance of a Poisson distribution is also lambda. For Example 1, the variance of 4.151515 is not too different from the lambda value of 3.166667.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Penn State (2024) Maximum likelihood estimation
https://online.stat.psu.edu/stat504/Lesson01#maximum-likelihood-estimation
Wikipedia (2024) Poisson distribution
https://en.wikipedia.org/wiki/Poisson_distribution