Basic Concepts
The log-likelihood function for a sample {x1, …, xn} from a lognormal distribution with parameters μ and σ is
![]()
The log-likelihood function for a normal distribution is
Thus, the log-likelihood function for a sample {x1, …, xn} from a lognormal distribution is equal to the log-likelihood function from {ln x1, …, ln xn} minus the constant term ∑lnxi. Since the constant term doesn’t affect which parameter values produce the maximum value of LL, we conclude that the maximum is achieved for the same values of μ and σ on the sample {ln x1, …, ln xn} taken from a normal distribution, namely
![]()
A less biased value of σ2 is obtained by replacing n with n–1.
Click here for more details about the LL formula and the estimation of μ and σ via MLE.
Example
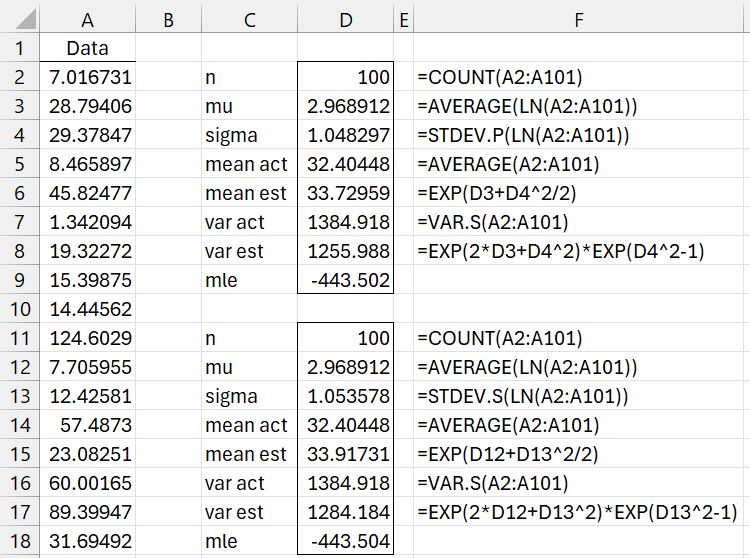
Example 1: Repeat Example 1 from Method of Moments: Lognormal Distribution using MLE. The data containing 100 elements is repeated in column A of Figure 1 (only the first 17 elements are displayed).
Figure 1 – Fitting a lognormal distribution
Cell D9 contains the formula
=-D2*(LN(2*PI())/2+LN(D4)+(D3/D4)^2/2)+(D3/D4^2-1)*SUM(LN(A2:A101))-SUMSQ(LN(A2:A101))/(2*D4^2)
The results are shown on the upper right side of the figure. We see that the mu and sigma values are slightly different from the values estimated using the method of moments. The LL of -443.502 (cell D9) is a little better than the LL of -445.992 for the method of moments.
If we use the less biased version of σ2, as suggested above, the LL is only reduced to -443.504, as shown on the lower right side of the figure.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Genos, B. F. (2009) Parameter estimation for the Lognormal distribution
https://scholarsarchive.byu.edu/cgi/viewcontent.cgi?article=2927&context=etd
Wikipedia (2020) Log-normal distribution
https://en.wikipedia.org/wiki/Log-normal_distribution
Pavlovic, M. (2022) Formulas & proofs for the log-normal distribution
https://majapavlo.github.io/blog/2022/02/02/lognorm_formulas.html
Thanks for the great resource shared, Charles. How do you formulate the likelihood function for lognormal distribution with right censored data?
Happen to notice that the log-likelihood function stated on this page mismatches with the same LL function on the linked details page.
https://real-statistics.com/distribution-fitting/distribution-fitting-via-maximum-likelihood/fitting-lognormal-distribution-via-mle/fitting-lognormal-distribution-details/
Hi,
Thanks for your kind remarks about Real Statistics.
1. I haven’t tried to formulate the likelihood function for lognormal distribution with right censored data. The approach is the same as that used for the Weibull distribution. See https://real-statistics.com/distribution-fitting/distribution-fitting-via-maximum-likelihood/weibull-censored-data/
2. Thanks for catching the error in the second line of the LL function on this webpage, The formula on the linked details page is correct.
Note that -(n/2)lnσ^2 = -nlnσ, and so that is not a problem. -nμ^2/σ^2 should be -nμ^2/(2σ^2). That is the error. In any case, I simply deleted the second line of the LL function on this webpage since I didn’t need to use it anyway.
I appreciate your support and your help.
Charles
the transformation y = exp(x) where x~N(m,s) has jacobian determinant 1/y, which does not depend on parameters and therefore is just a constant in the loglikelihood. In other words: to estimate m and s from y1…yn~lognormal(m,s):
1. take x_i = log(y_i) for all i =1,…,n
2. fit the normal model on all x_i
Hello, how can I estimate suning solver the parameters of Log normal and poisson distribution?
Hello,
I show how this is done for the Weibull distribution at
https://www.real-statistics.com/distribution-fitting/distribution-fitting-via-maximum-likelihood/fitting-weibull-parameters-mle/
The approach is similar for other distributions. For the Log-Normal distribution, you can find the formula for the Log-Likelihood function at
https://www.real-statistics.com/distribution-fitting/distribution-fitting-via-maximum-likelihood/fitting-lognormal-distribution-via-mle/
Charles