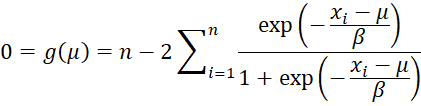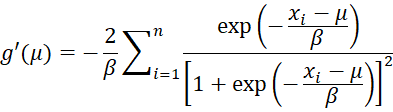Basic Concepts
The log-likelihood function for the Logistic distribution for the sample {x1, …, xn} is
![]()
![]()
To find the maximum value we need to solve the following equations simultaneously (the proof requires calculus).
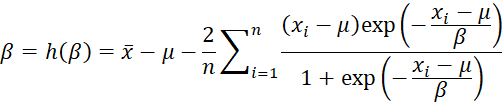
As we show for fitting the Gumbel distribution (see Fitting Gumbel Parameters via MLE), we can use a fixed point iteration to find a better version of beta for a given value of mu, namely
For any given value of beta, we can use Newton’s method to find a better version of mu, namely
We start with the values of mu and beta based on the method of moments. Then we use Newton’s method to obtain a better version of mu. We then use the fixed point iteration to obtain a better version of beta, repeating the process again and again until the estimates for mu and beta don’t change much.
Example
Example 1: Estimate the values of mu and beta that best fit a logistic distribution to the data in column A of Figure 1.
The sample size, mean, and standard deviation of the data are shown in range D3:D5. From these values, the values of mu and beta can be estimated by the method of the moments by μ = x̄ = 1.371849 and β = s√3/π= 1.687061, as shown in cells D7 and D8.
Figure 1 – Estimating logistic distribution parameters
The right side of the figure shows how to estimate these parameters, iteratively, using the MLE approach. The first 2 steps and the last 2 steps out of the 9-step iteration are shown. We now describe the formulas for step 1 shown in columns G and H, and how to extend these to columns I through Z.
Cells G2 and G3 are copied from the method of moments estimates in cells D7 and D8. Cell G4 contains the formula =EXP((G$2-$A4)/G$3) (corresponding to the first data element in cell A4). When range G3:Z18 is highlighted and Ctrl-D and Ctrl-R are pressed, similar formulas are used to fill the highlighted range.
The log-likelihood based on the initial guess is -37.932 (cell G20) using the formula
=$D$3*G2/G3-$D$3*$D$4/G3-2*SUMPRODUCT(LN(G4:G18+1))-$D$3*LN(G3)
Highlighting the range G20:Z18 and pressing Ctrl-R fills in the LL values for the subsequent iterations, ending in LL = -37.9193, which is larger than the value in cell G20, showing that the estimate based on MLE is better than that based on the method of moments.
Newton’s Method
We now try to obtain a better estimate for mu (i.e. one whose LL value, in cell H20, is larger) assuming the initial beta value is fixed. This is done by placing the formula =G2-G21/G22 in cell G23 where G21 contains the formula =$D$3-2*SUMPRODUCT(G4:G18,1/(G4:G18+1)) and G22 contains the formula =-2*SUMPRODUCT(G4:G18,1/(1+G4:G18)^2)/G3. This represents one step in Newton’s method. The result is a new value for mu shown in cell G23. The beta value is not changed (i.e. cell G24 contains =G3). We now copy the new mu value into cell H2 (via =G23) and retain the previous beta value in cell H3.
Next, we update the beta value using the fixed point expression by placing the formula
=$D$4-H2-2*SUMPRODUCT($A4:$A18-H2,H4:H18,1/(H4:H18+1))/$D$3
in cell H24 and the formula =(H3+H24)/2 in cell I3, keeping the previous mu value in cell I2. We now highlight range I2:Z3 and press Ctrl-R and copy range G21:H24 into I21:J24 and then into K21:L24, …, Y21:Z24.
After 9 iterations, we have a reasonable level of convergence, obtaining the values μ = 1.446974 and β = 1.73217.
Note that the original data values in Figure 1 were obtained from a Logistic distribution with parameters μ = 1 and β = 2, using the formula =LOGISTIC_INV(RAND(),1,2,TRUE). Since the sample was quite small, the estimated parameter values from the MLE method are not especially accurate.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Taboga, M. (2021) Logistic model maximum-likelihood estimation
https://www.statlect.com/fundamentals-of-statistics/logistic-model-maximum-likelihood
Millard, S. P. (2023) Estimate parameters of a logistic distribution
https://search.r-project.org/CRAN/refmans/EnvStats/html/elogis.html
Forbes, C., Evans, M., Hastings, N., Peacock, B. (2011) Statistical distribution. Wiley
https://www.academia.edu/49056503/Statistical_distributions