Basic Concepts
The log-likelihood function for the Geometric distribution for the sample {x1, …, xn} is
The MLE value is achieved when
which is the same value as from the method of moments (see Method of Moments).
Example
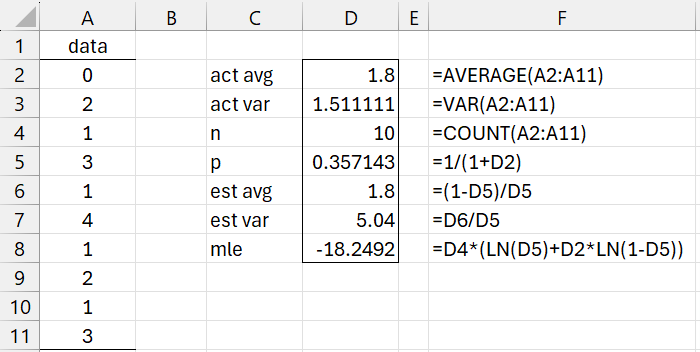
Example 1: Estimate the p parameter for a geometric distribution that best fits the data in range A2:A11 of Figure 1.
Figure 1 – Fitting a geometric distribution
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Forbes, C., Evans, M., Hastings, N., Peacock, B. (2011) Statistical distribution. Wiley
https://www.academia.edu/49056503/Statistical_distributions
Siegrist, K. (2022) Maximum-Likelihood
https://stats.libretexts.org/Bookshelves/Probability_Theory/Probability_Mathematical_Statistics_and_Stochastic_Processes_(Siegrist)/07%3A_Point_Estimation/7.03%3A_Maximum_Likelihood
Millard, S. P. (2023) Estimate probability parameter of a geometric distribution
https://search.r-project.org/CRAN/refmans/EnvStats/html/egeom.html