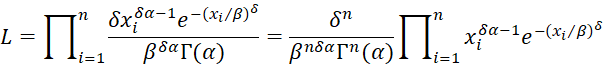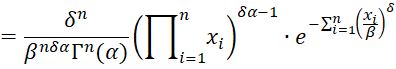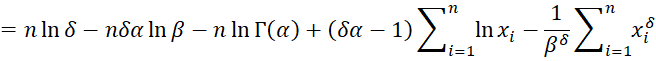Basic Concepts
If we have a sample x1, …, xn that we suspect follows a generalized gamma distribution, we can estimate the parameters of this distribution by maximizing the value of the log-likelihood function.
The likelihood function is
Thus, the log-likelihood function is
Example
Example 1: Repeat Example 1 of Method of Moments: Generalized Gamma Distribution using Maximum Log-Likelihood Estimation (MLE).
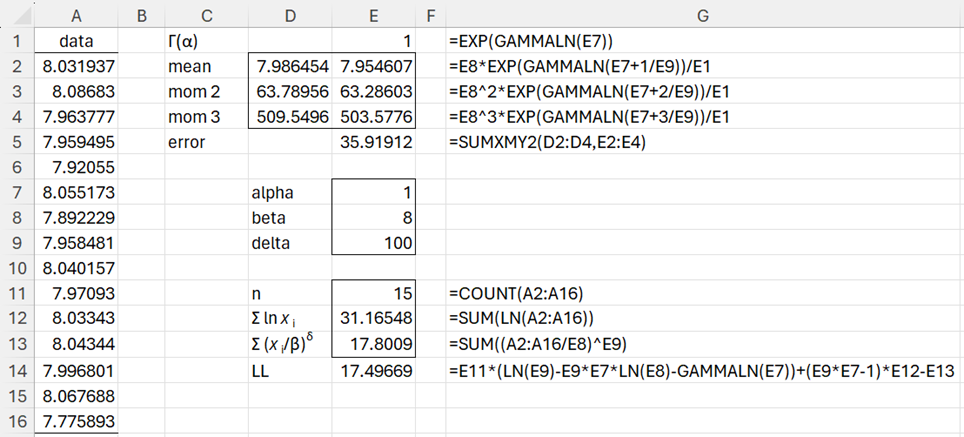
We accomplish this via Excel’s Solver using the spreadsheet shown in Figure 1 where A2:A16 contains the data for Example 1.
Figure 1 – Setup for using Solver
Here cell E14 contains the value of LL for the initial parameter guesses shown in E7:E9. Our objective is to change the parameter values in E7:E9 to maximize the value in cell E14. We do this by selecting Solver and filling in the Solver dialog box shown in Figure 2.
Figure 2 – Upper portion of Solver dialog box
After clicking on the Solve button, the spreadsheet in Figure 1 changes to that shown in Figure 3.
Figure 3 – Improved fit based on LL
We see that the LL has increased from 17.49669 to 19.25938.
As we did when using the method of moments, we could try to use Solver’s Multistart capability to improve on these results. When we did this, however, we didn’t obtain a substantially different solution.
Notice that, not surprisingly, the LL value of 19.25938 here is a little higher than the LL value of 19.11681 obtained using the method of moments (see Figure 5 of Method of Moments: Generalized Gamma Distribution). The moments are a little closer fit when using the method of moments (error of .0000000461 versus .001364).
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Nematrian (2023) The generalised gamma distribution
http://www.nematrian.com/GeneralisedGammaDistribution
Jimenez Nava, V. H. (2011) Gamma and generalized gamma distributions
https://scholarworks.utep.edu/open_etd/2321/