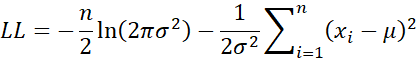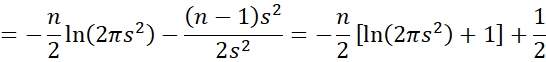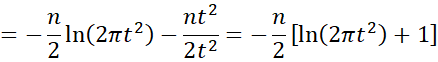Fitting a Normal Distribution via MLE

Basic Concepts

The normal distribution is characterized by two parameters: the mean μ and standard deviation σ (or variance σ²). Using the method of moments, we can estimate the distribution mean by the sample mean. We estimate the distribution standard deviation by the sample standard deviation.

Using the maximum likelihood estimation, once again, we estimate the distribution mean by the sample mean. We estimate the standard deviation by the sample standard deviation but with division by n instead of n-1 (i.e. using VAR.P instead of VAR.S in Excel).

Log-likelihood Estimate

For a sample x₁, …, x_n, the log-likelihood is 

when we use the sample variance s² to estimate σ² (method of moments approach). For the MLE approach, when the modified sample variance t² is used, we get

Recall that s² is an unbiased estimate of the variance, while t² is a biased estimate (see Properties 3 and 7 of Estimators.

Example

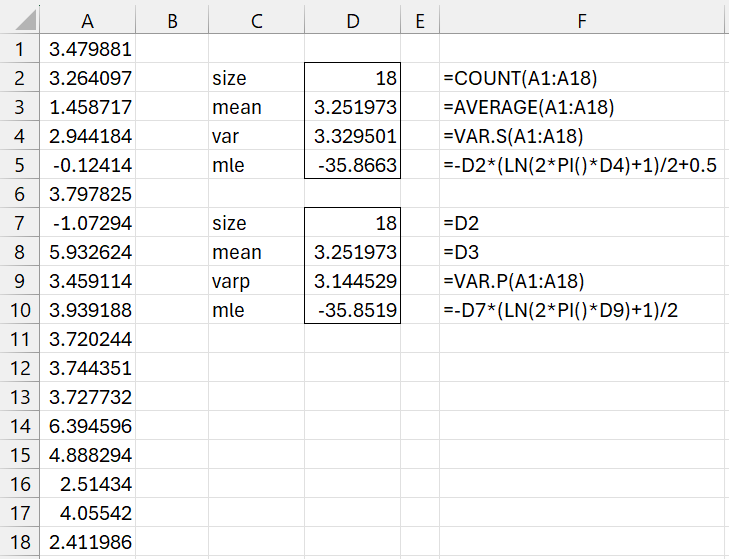
Example 1: Estimate the mu and sigma parameters for a normal distribution that best fits the data in range A1:A18 of Figure 1. Use both the method of moments and MLE.

Figure 1 – Fitting a normal distribution

We display the MoM estimation on the upper right part of the figure and the MLE on the lower right part.

Links

↑ MLE Fit

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Wikipedia (2024) Maximum likelihood estimation
https://en.wikipedia.org/wiki/Maximum_likelihood_estimation

Carnegie Mellon University (2024) Maximum Likelihood Estimation
Article no longer available online