Distribution Fitting via MLE: Real Statistics Support

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack contains the following array functions that estimate the appropriate distribution parameter values (plus the actual and estimated mean and variance as well as the MLE value) which provide a fit for the data in R1 based on the MLE approach; R1 is a column array with no missing data values.

BETA_FIT(R1, lab, iter, aguess, bguess) = returns an array with the beta distribution parameter values alpha, beta, actual and estimated mean and variance, and MLE.

CAUCHY_FIT(R1, lab, iter, sguess, mguess) = returns an array with the Cauchy distribution parameters mu, sigma, median, 76% trimmed mean, inclusive IQR, exclusive IQR, and MLE

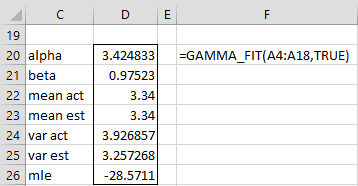
GAMMA_FIT(R1, lab, iter, aguess) = returns an array with the gamma distribution parameter values alpha, beta, actual and estimated mean and variance, and MLE.

GEV_FIT(R1, lab, iter, prec, incr, mguess, sguess, xguess): returns a 3 × 4 array; the first column of the output contains the estimated values for μ, σ, ξ; the second column contains error values (values near zero indicate that the iteration has converged successfully); the third column contains the standard errors of the parameter estimates; the fourth column contains the MLE value based on the estimated parameter values.

GUMBEL_FIT(R1, lab, iter, bguess) = returns an array with the Gumbel distribution parameter values mu, beta, actual and estimated mean and variance, and MLE.

LOGISTIC_FIT(R1, lab, iter, bguess, mguess) = returns an array with the Logistic distribution parameter values mu, beta, actual and estimated mean and variance, and MLE.

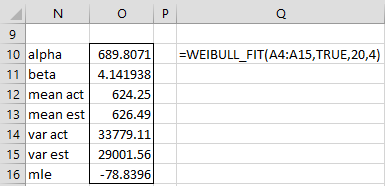
WEIBULL_FIT(R1, lab, iter, bguess) = returns an array with the Weibull distribution parameter values alpha, beta, actual and estimated mean and variance, and MLE.

Functions without guess arguments

EXPON_FIT(R1, lab) = returns an array with the exponential distribution parameter value lambda, sample variance, actual population variance, estimated variance, and MLE.

GEOM_FIT(R1, lab) = returns an array with the geometric distribution parameter value p, sample variance, actual population variance, estimated variance, and MLE.

LAPLACE_FIT(R1, lab) = returns an array with the Laplace distribution parameter values mu, beta, sample variance, actual population variance, estimated variance, and MLE.

NEGBINOM_FIT(R1, lab) = returns an array with the negative binomial distribution parameter values k, p, actual and estimated mean and variance, and MLE. k takes an integer value between 2 and 1,000.

PARETO_FIT(R1, lab) = returns an array with the Pareto distribution parameter values alpha, min, sample variance, actual population variance, estimated variance, and MLE. 

UNIFORM_FIT(R1, lab, iter) = returns an array with the uniform distribution parameter values alpha, beta, actual and estimated mean and variance, and MLE.

Function Parameters for GEV_FIT

If lab = TRUE (default FALSE) then an extra row and an extra column of labels are appended to the output. 

mguess, sguess, xguess are the initial guesses for mu, sigma, and xi. If sigma = 0 (default), then the initial guesses for all three parameters come from the method of moments; otherwise, the mu defaults to 0, and xi defaults to -.1.

iter (default 100) = the maximum number of iterations. The algorithm will terminate prior to iter iterations once the error is less than prec (default .0000001). incr is used to calculate the derivative of the log-likelihood function and defaults to .000001.

Function Parameters for other Functions

If lab = TRUE, then an extra column of labels is appended to the output (default is FALSE).

iter is the number of iterations used in calculating the solution (default 20, except for GUMBEL_FIT and LOGISTIC_FIT where the default is 25). For UNIFORM_FIT if iter = 0 then alpha and beta are set to the minimum and maximum data values (biased MLE).

mguess, sguess, aguess, and bguess are the initial guesses used for the mu, sigma, alpha, and beta parameters (default 0, which means that the function uses an internal algorithm to make the initial guess, often the estimates based on the method of moments).

Auxiliary Worksheet Function

In calculating BETA_FIT and GAMMA_FIT, the following Real Statistics function is used:

POLYGAMMA(z, k) = digamma function at z if k = 0 (default), and trigamma function at z if k = 1.

MLE for Triangular and PERT distributions

You can use the TRIANG_FIT and PERT_FIT worksheet functions to fit data to the triangular and PERT distributions using MLE. These functions have a different format from the functions described above. You can obtain a complete description of these functions by clicking on the links associated with these functions. 

Examples

For example, we can calculate the results for Example 1 of Fitting Weibull Parameters via MLE as shown in Figure 1.

Figure 1 – WEIBULL_FIT

We can also calculate the results for Example 1 of Fitting Gamma Parameters via MLE as shown in Figure 2.

Figure 2 – GAMMA_FIT

There is also a version of the WEIBULL_FIT function that handles censored data, as described in Weibull with Censored Data.

See Fitting a GEV Distribution via MLE for an example of GEV_FIT.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Wikipedia (2017) Maximum likelihood estimation
https://en.wikipedia.org/wiki/Maximum_likelihood_estimation

Forbes, C., Evans, M., Hastings, N., Peacock, B. (2011) Statistical distribution. Wiley
https://www.academia.edu/49056503/Statistical_distributions