Distribution Fitting Tool

We now show how to use Real Statistics capabilities to determine the fit of data to various probability distributions.

Set-up

Real Statistics Data Analysis Tool: You can use the Real Statistics Distribution Fitting data analysis tool to determine the fit of data to a normal, Weibull, exponential, beta, gamma, Gumbel, logistic, log-normal, geometric, Laplace, or uniform distribution. For the Weibull distribution, censored data is supported as well.

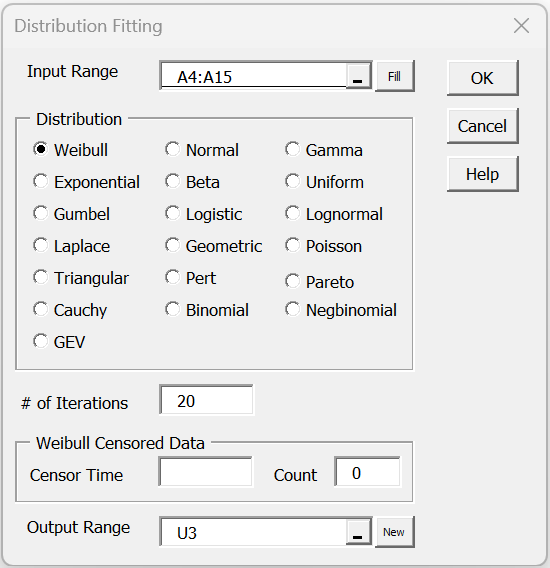
For example, to use this data analysis tool for Example 1 of Fitting Weibull Parameters via MLE, press Ctrl-m and select the Distribution Fitting option from the dialog box that appears (or from the Misc tab if using the Multipage user interface). Next fill in the dialog box that appears as shown in Figure 1.

Figure 1 – Distribution Fitting dialog box

Output

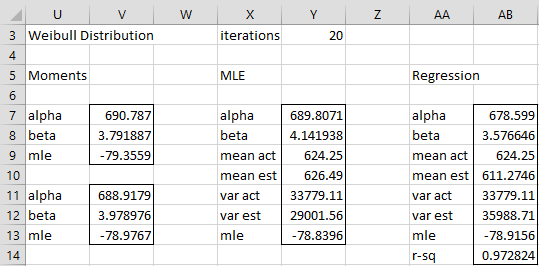
Upon clicking on the OK button the output shown in Figure 2 is displayed.

Figure 2 – Weibull Distribution Fitting output

To perform Example 1 of Weibull with Censored Data, you follow the same steps, except that you need to fill in the Count field in Figure 1 with the number 2 and the Censor Time field with 900.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Wikipedia (2017) Maximum likelihood estimation
https://en.wikipedia.org/wiki/Maximum_likelihood_estimation

Wikipedia (2021) Method of moments (statistics)
https://en.wikipedia.org/wiki/Method_of_moments_(statistics)

Hastings, N., Peacock, B. (2011) Statistical distributions. 4th Ed, Wiley
https://www.wiley.com/en-us/Statistical+Distributions%2C+4th+Edition-p-9780470390634