Basic Concepts
Suppose that we have used one of the techniques described on this website to fit data to some distribution. We can obtain estimates of the standard error for the fitted parameters by using bootstrapping. In this approach, we generate a large number (say k = 1,000) of random samples of the distribution using the fitted parameters where each sample has the same size as the original sample.
For any parameter β, if the fitted parameter values for each of the k samples are β1, …, βk with mean β-bar, then the standard error of the β parameter is estimated as
Example
Example 1: For Example 1 of Fitting Gumbel Parameters via MLE, using the MLE method we estimate that the data could be fit by a Gumbel distribution with parameters μ = 2.11332 and β = 349323. Determine the precision of these estimates by estimating the standard errors of the parameter estimates.
To illustrate the process, we will base the standard errors on 10 samples, although generally, we would use many more samples. This is shown in Figure 1.
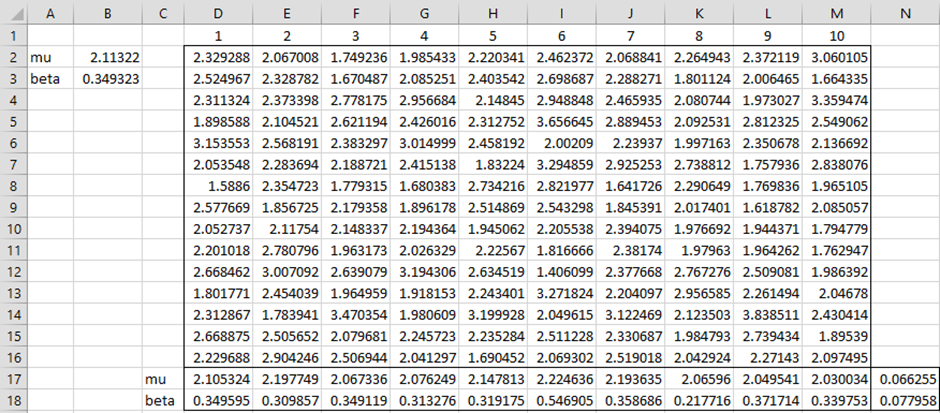
Figure 1 – Standard error for Gumbel parameters
We estimate standard errors for mu of 0.066255 (cell N17) and for beta of .077958 (cell N18). These values are obtained by first inserting the formula =GUMBEL_FIT(RAND(),$B$2,$B$3) in cell D2, highlighting the range D2:M16 and pressing Ctrl-R and Ctrl-D. This results in 10 random samples each of size 15, the size of the original sample.
We now insert the array formula =GUMBEL_FIT(D2:D16) in range D17:D18, highlight the range D2:M18, and press Ctrl-R, resulting in 10 values for mu and beta. The bootstrapped standard error for mu, shown in cell N17, is the (population) standard deviation of the 10 mu values, as calculated by the formula =STDEV.P(D17:M17). Similarly, the standard error for beta is calculated by the formula =STDEV.P(D18:M18) in cell N18.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Tibshirani, R. (2014) The bootstrap. Advanced methods for data analysis
https://www.stat.cmu.edu/~ryantibs/advmethods/notes/bootstrap.pdf
