3-level design overview
We now consider the following fractional 3^k designs. These designs are generally limited to three levels, which are labelled 1, 2 and 3 (although we include one design that accepts one 6-level factor).
Figure 1 – Three-level designs
The first two of these designs only use 3-level factors. These support interactions as described below.
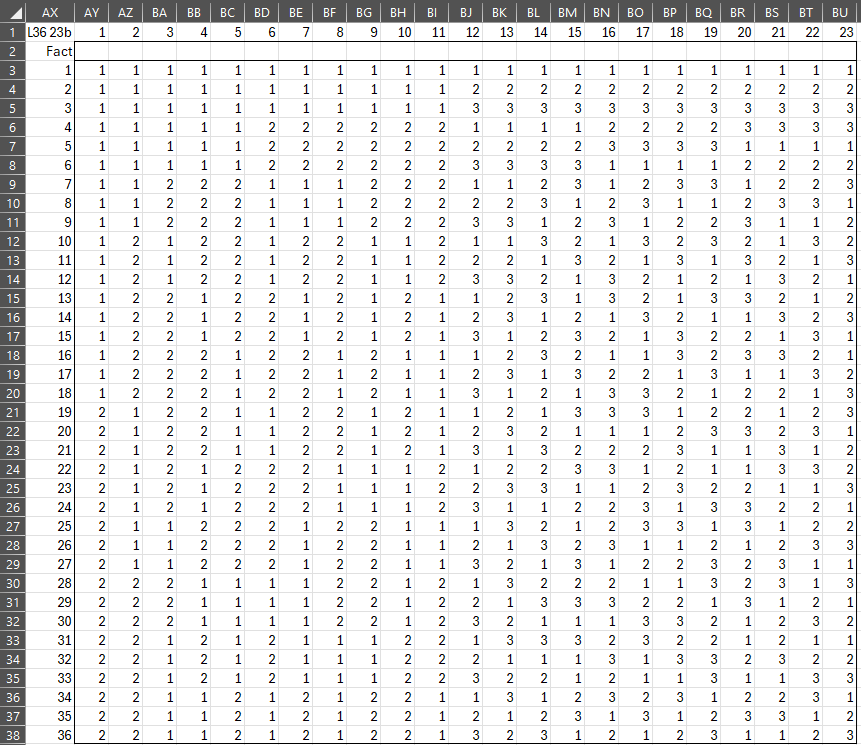
The next four designs allow a combination of 2-level and 3-level factors without interactions. The L18 63 design uses the first column for a 6-level factor and the rest for 3-level factors. The L18 23 and L54 23 designs use the first column for a 2-level factor and the rest for 3-level factors. The L36a and L36b designs allow for more 2-level factors with the columns allocated to 2-level factors preceding those allocated to 3-level factors.
3-level designs
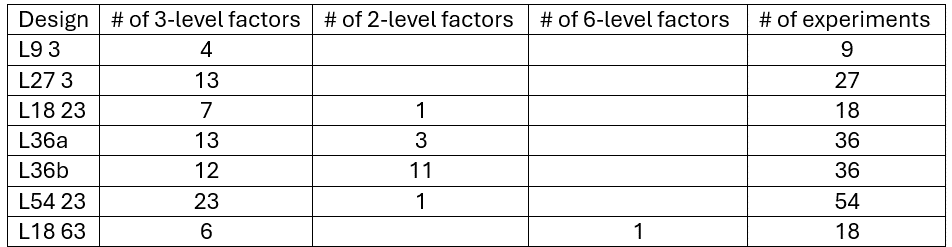
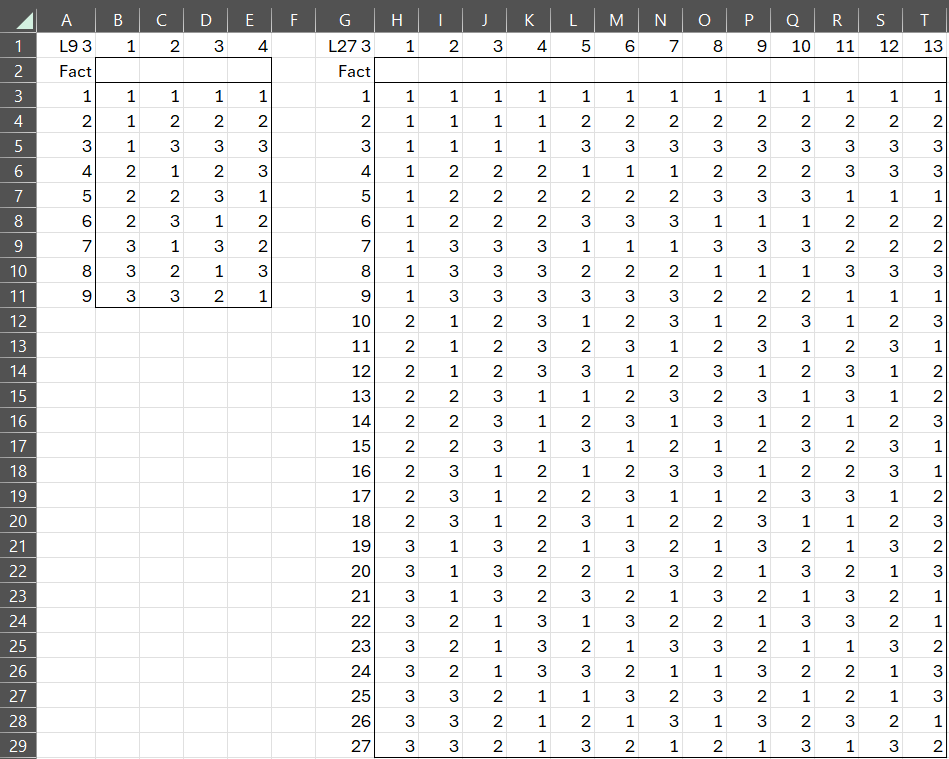
The L9 and L27 designs are shown in Figure 2.
Figure 2 – L9 3 and L27 3 designs
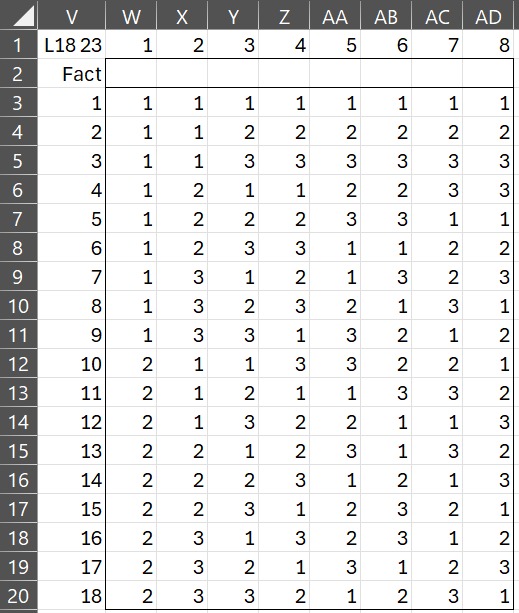
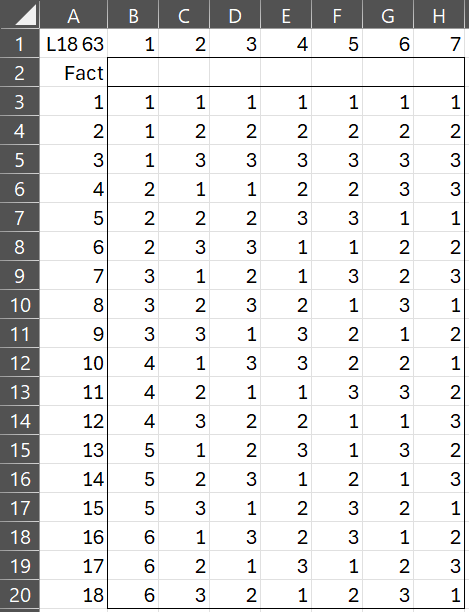
The other designs are shown in Figures 3, 4, 5, 6, and 7.
Figure 3 – L18 23 design
Figure 4 – L18 63 design
The following two designs support multiple 2 and 3-level factors.
Figure 5 – L36a design
Figure 6 – L36b design
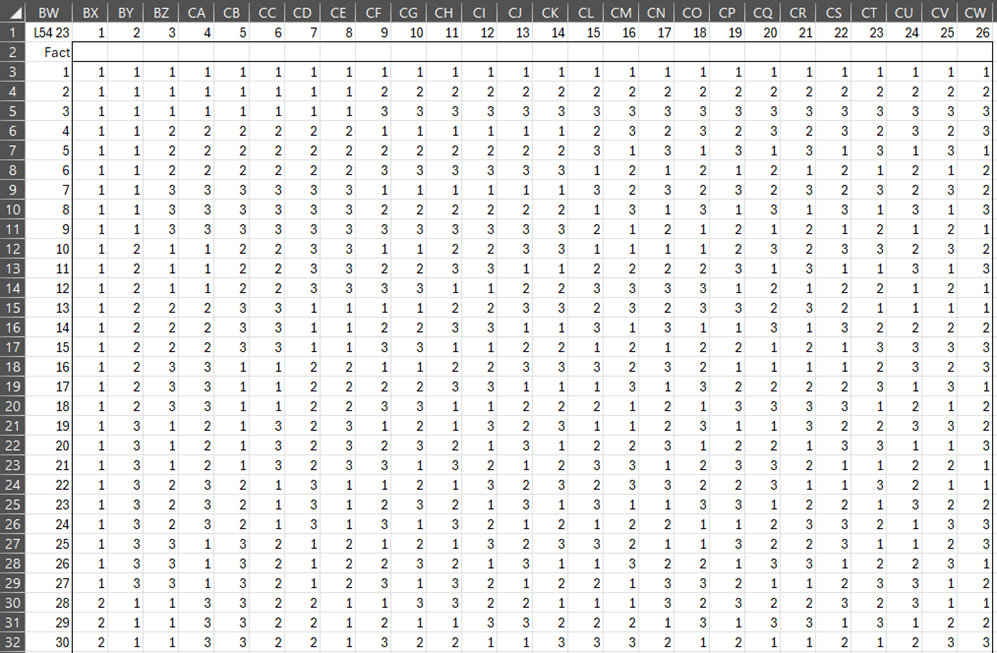
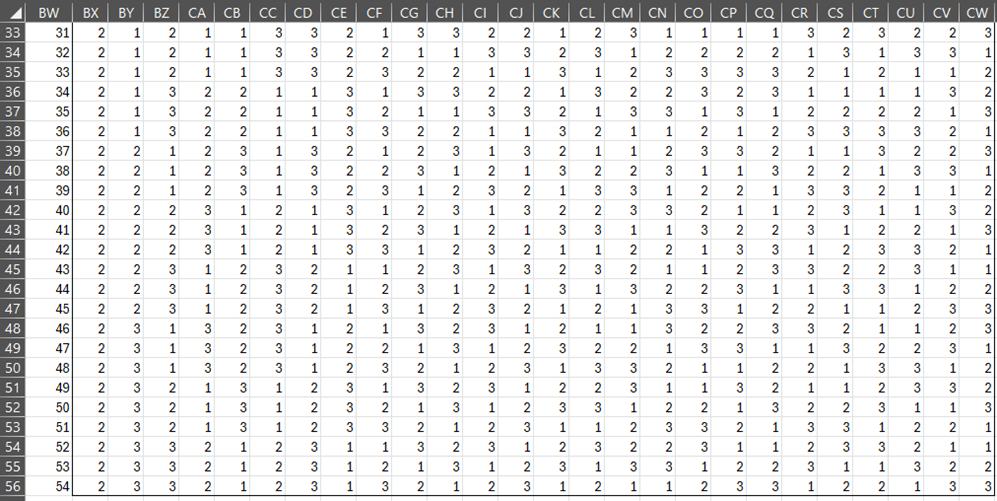
The following figure supports up to 25 3-level factors.
Figure 7 – L54 23 design
Interactions
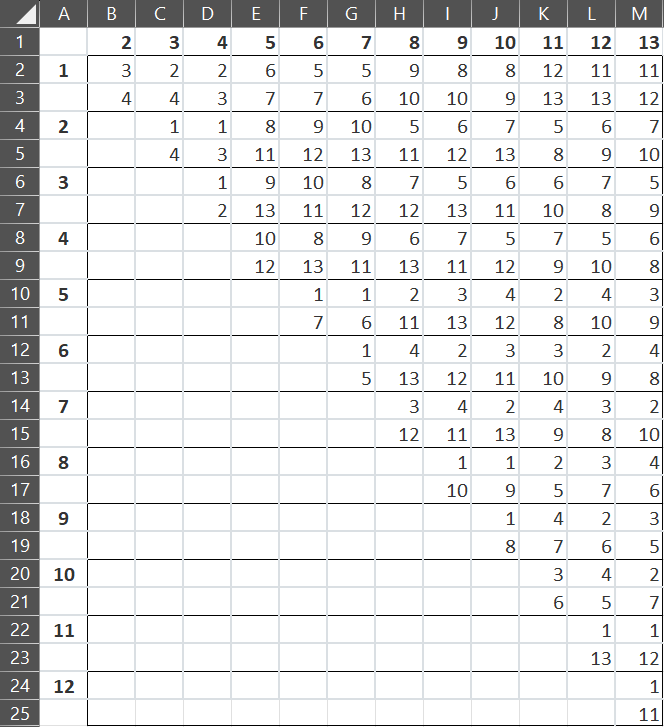
The L9 and L27 designs permit interaction factors as described in Figure 8. Note that the interactions take up two columns in the design, not one as for the 2-level factor designs.
Figure 8 – Interactions for 3-level designs
E.g. if we are using the L27 design and assign factor B to column 2 and factor C to column 5, then we need to assign the interaction factor BC to columns 8 and 11.
We can also use the TInteract function described in Signal-to-Noise Ratio to obtain this result. Here, the array formula =TInteract(2,5,3) outputs a 1 × 2 row array with the values 8 and 11. The last argument in the formula specifies the levels, namely 3.
Examples
Click here for two examples of creating a 3-level Taguchi design.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Roy, R. K. (2010) A primer on Taguchi method. 2nd ed. Society of Manufacturing Engineers
https://brharnetc.edu.in/br/wp-content/uploads/2018/11/11.pdf
University of York (2004) Orthogonal arrays (Taguchi designs)
https://www.york.ac.uk/depts/maths/tables/orthogonal.htm
Minitab (2024) Catalogue of Taguchi designs
https://support.minitab.com/en-us/minitab/help-and-how-to/statistical-modeling/doe/supporting-topics/taguchi-designs/catalogue-of-taguchi-designs/