Split-plot Tools

Example 1: A manufacturer of plastics is exploring four different compositions for a new type of plastic and wants to determine which yields a plastic with more flexibility. It is also interested in determining which of three temperature levels during the manufacturing process produces the best result.

Thus, there are 4 × 3 = 12 different combinations of the two factors. The manufacturer has dedicated one production facility to this test for three days and this facility runs 4 shifts a day and is capable of 3 runs per shift.

Since it is difficult to change the process for creating each composition, the decision was made to produce one such composition per shift, randomly choosing the order of the 4 compositions among the 4 shifts. In any one shift, a batch of the selected composition is split into 3 parts each of which is heated to a different one of the 3 temperatures.

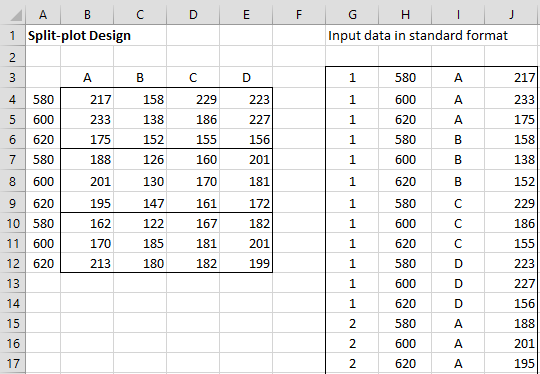
The level of flexibility of the plastic for each run is as described in range A3:E12 of Figure 1.

Figure 1 – Split-plot design input

Here the columns represent compositions and the rows represent the temperatures. The values in the cells are the measurements of flexibility.

Note that this design is different from a completely randomized design. In that case, on each day 12 batches would be created, and that batch would use one of the 12 combinations of composition and temperature, for a total of 36 batches over the 3 days.

The design used for this example (i.e. a split-plot design) creates only 3 batches per day, where each day is a block (i.e. a replication) and where each batch corresponds to a main treatment (i.e. main plot), which is divided into 4 sub-treatments (i.e. subplots).

The layout on the left side of Figure 1 represents the data in Excel format, with the columns corresponding to whole plots and the rows to subplots. The layout on the right side of Figure 1 is the same data in standard (i.e. stacked format), although only the first 15 of 36 rows is displayed.

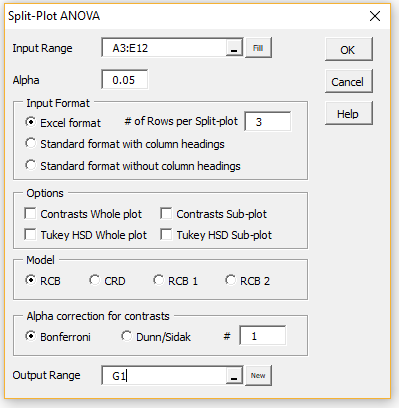
To conduct the analysis we use Real Statistics’ Split-plot Anova data analysis tool. To access the tool, press Crtl-m, choose the Analysis of Variance option and then select the Split-plot Anova option. You now fill in the dialog box that appears as shown in Figure 2.

Figure 2 – Split-plot Anova dialog box

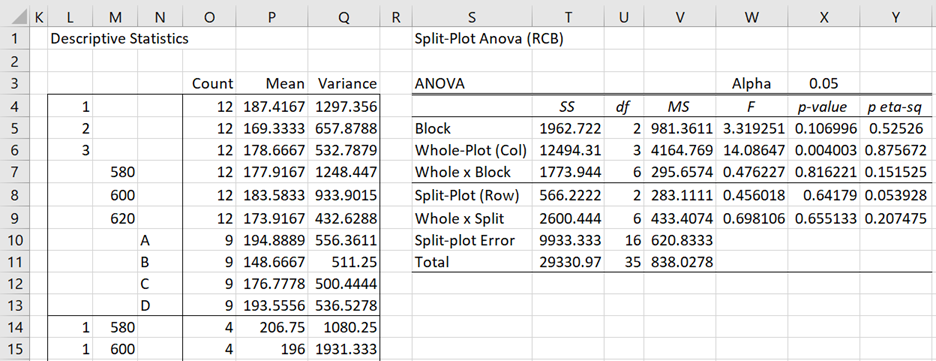
We choose the Excel format option using the RCB model for whole plots with 3 rows per replication. The data analysis tool first converts the data in Excel format into standard format (as shown in range G1:J34 of Figure 1), and then outputs the descriptive statistics and Anova shown in Figure 3. If the input data is already in standard format you would choose the Standard format with column headings or Standard format without column headings and obviously the conversion to standard format would not be necessary.

Figure 3 – Split-plot analysis

The descriptive statistics are as for three-factor Anova described in Real Statistics Support for Three Factor ANOVA (with only the first 12 rows shown in Figure 3). Looking at the Anova results, we see that there is a significant difference among the four compositions (cell Y6), but not among the temperatures (cell Y8) or in the interactions between the composition and temperature factors (cell Y9).

The formulas for the sum of squares and degrees of freedom portion of Figure 3 are given in Figure 4.

Figure 4 – Sum of squares and df formulas from Figure 3

Note that cell O83 contains the formula =SUM(O47:O82) and cell Q83 contains the formula =VAR(J3:J38).

MS of Whole × Block (cell V7) is the error term for the Block and Whole Plot factors, and so F for Block (cell F5) can be calculated by the formula =V5/V7 and F for Whole Plot (cell F6) can be calculated by the formula =V6/V7. MS of the Split-plot error (cell V10) is the error term for Whole Plot × Block, Subplot and Whole plot × Subplot.