Split-plot Follow-up Tests

As for Randomized Complete Block Design, described in Follow-up RCBD Testing, the Split-plot Anova data analysis tool provides support for two follow-up tests: Contrasts and Tukey HSD.

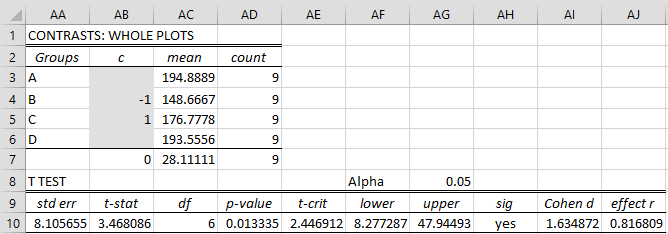
Example 1: As we see from Figure 3 (cell Y6) of Split-plot Tools, there is a significant difference between the whole plot factors (composition) in Example 1 of Split-plot Tools. Use contrasts to determine whether there is a significant difference between compositions B and C.

You can accomplish this analysis, by choosing the Split-plot Anova data analysis tool and checking the Contrasts Whole plot option on the dialog box as shown in Figure 2 of Split-plot Tools. After filling in the contrast coefficients in range AB3:AB6 of Figure 1, we get the following analysis.

Figure 1 – Whole plot contrasts

We see that there is a significant difference between the flexibility values for compositions B and C.

The formula for the standard error (cell AA10) is

=SQRT(V7*SUMPRODUCT(AB3:AB6^2,1/AD3:AD6))

This formula refers to the Whole Plot MS_E (cell V5 in Figure 3 of Split-plot Tools). Similarly, the df_E (AC10) is calculated using the formula =U7.

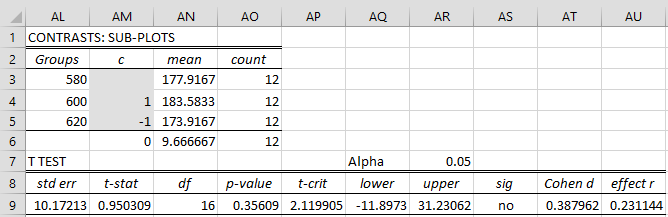
We can also perform contrast analysis on subplots (see Figure 2) by choosing the Contrasts Sub-plots option on the Split-plots Anova dialog box (see Figure 2 of Split-plot Tools), although for Example 1 of Split-plot Tools this not necessary since as we have seen from Figure 3 of Split-plot Tools there is no significant difference between the flexibility values based on temperature.

Figure 2 – Subplot contrasts

Note that for the subplot contrasts, the worksheet formula for the df (cell AN9) and standard error (cell AL9) are =U10 and =SQRT(V10*SUMPRODUCT(AM3:AM5^2,1/AO3:AO5)). These formulas refer to the Subplot df_E and MS_E (cell U10 and V10 in Figure 3 of Split-plot Tools).

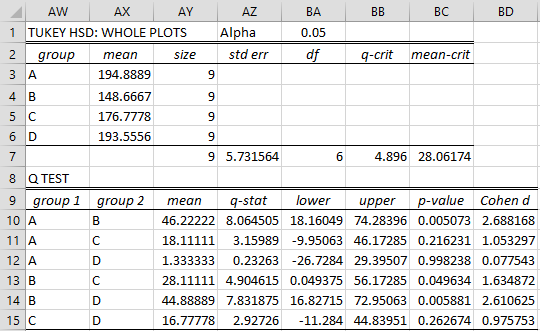
Example 2:  Use Tukey’s HSD to determine which pairs of compositions have a significant difference based on the data from Example 1 of Split-plot Tools.

This time we choose Tukey Whole plots option on the dialog box as shown in Figure 2 of Split-plot Tools to obtain the analysis shown in Figure 3.

Figure 3 – Tukey’s HSD for whole plots

From Figure 3, we see that p-value = .049634 < .05 = α, and so there is a significant difference between compositions B and C, and therefore between A and B and between B and D (since the difference between their means is larger). We also see that there is not a significant difference between any of the other pairs of compositions.

As for whole plot contrasts, this analysis uses the MS_E and df_E for the whole plots error term. E.g. cell AW10 contains the formula =SQRT(V7/AZ7) and cell AY contains the formula =U7.

We can also perform Tukey’s HSD for subplots by selecting the Tukey Sub-plot option, as shown in Figure 4.

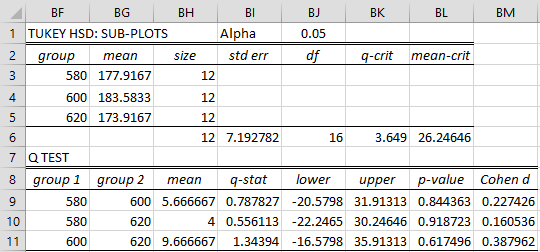
Figure 4 – Tukey’s HSD for sub-plots

The Split-plot Anova data analysis tool doesn’t provide a way to perform contrasts of Tukey’s HSD on the interaction between the whole plot and sub-plot factors. Instead, we need to use the Randomized Complete Block ANOVA data analysis tool.

Example 4: Determine whether there is a significant difference between the flexibility of compositions B and C at 580 degrees based on the data in Example 1 of Split-plot Tools.

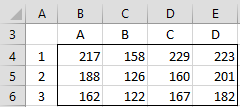
First, we need to eliminate the data for temperatures not equal to 580 degrees from Figure 1 of Split-plot Tools. This results in the data in Figure 5.

Figure 5 – Data at 580 degrees

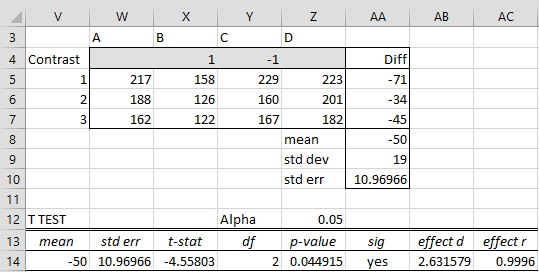
We now use the Contrasts option for the Randomized Complete Block ANOVA data analysis tool based on the input data in range A3:E6 of Figure 5. Filling in the appropriate contrast coefficients in the output, we get the analysis shown in Figure 6.

Figure 6 – Interaction contrast

We see that the differences between the means is 50, which is significant (cell AA14).

Note that this result is significant despite the fact that the Whole plot × Subplot interaction is not significant (see cell Y9 of Figure 3 of Split-plot Tools).