On this webpage, we describe the basic concepts about split-plot designs. See the following webpages for more details:
- Real Statistics data analysis tools for split-plot designs
- Support for other split-plot models
- Follow-up tests
In a split-plot design, we have two factors, a whole plot factor and a subplot factor. Each whole plot is divided into subplots. In the agricultural context this can be described as follows:
For example, if we study the effects of irrigation and fertilizer on the yield of barley, we can apply four types of irrigation techniques to the four fields (the whole plots) at random and then apply the three fertilizers to the subplots of each of the whole plots at random.
If we have two factors, A with three levels, B with two levels and two replications, then in a completely randomized design (CRD) we could have the following randomization:
Here, the 6 possible combinations of factors are randomly distributed with two replications per combination.
In a split-plot design with the whole plots organized as a CRD, we first assign factor A to the main plots at random:
We then assign factor B to the subplots at random; e.g. as
In a split-plot design with the whole plots organized as an RCBD, we first assign factor A in blocks to the main plots at random. Here, there are two blocks corresponding to the two replications.
We then assign factor B to the subplots at random; e.g. as
Split-plot designs are commonly used to analyze manufacturing processes. Here, the hard-to-change factor is applied to the processes modeled as whole plots, while the easier-to-change factor is applied to the processes modeled as subplots. Replications are supported as described in the following example; replications correspond to the blocks in such analyses.
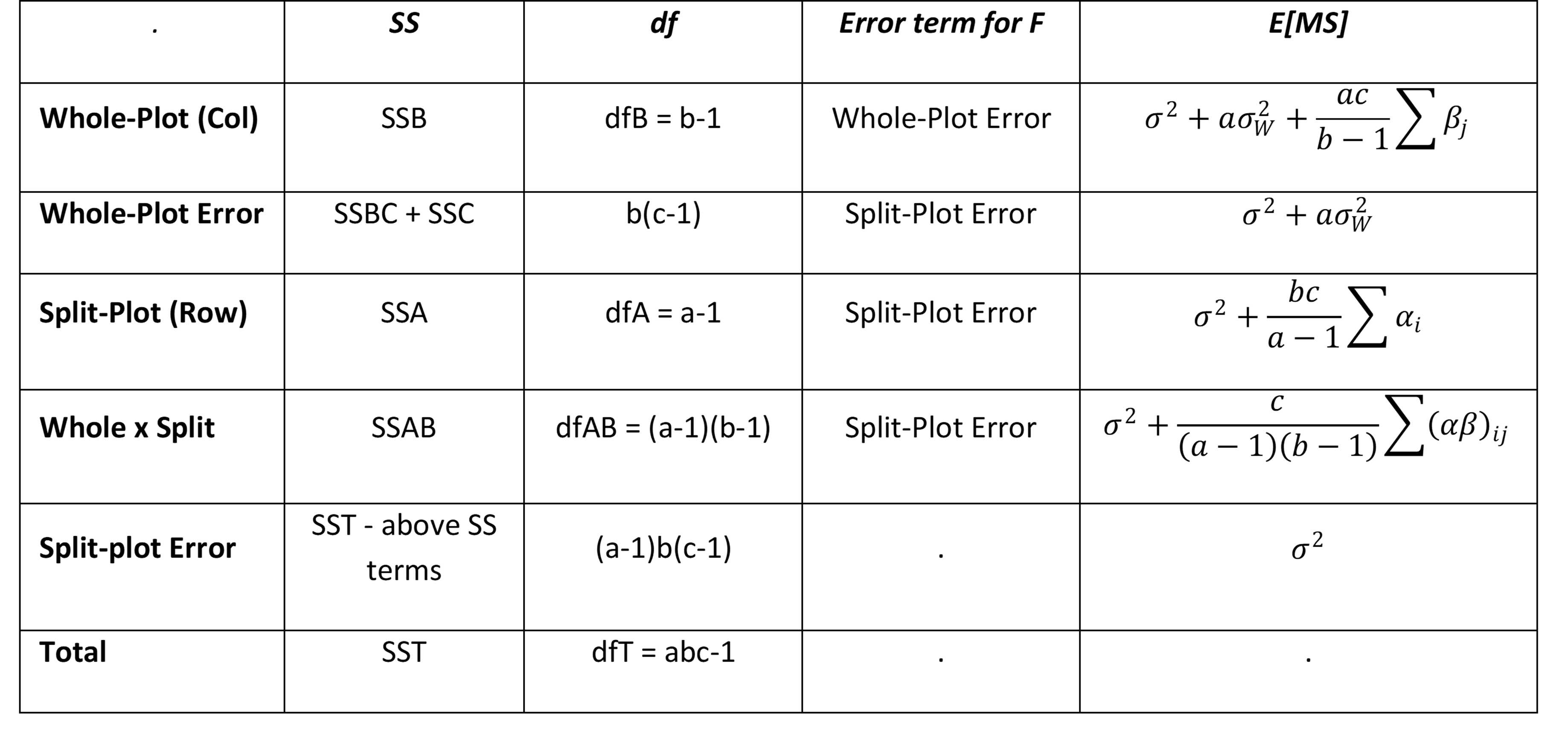
The model for Split-Plot with whole plots organized as CRD is
Here, factor A is the whole-plot factor with a levels, factor B is the split-plot factor with b levels, μ is the global mean, αi is the ith level whole-plot treatment effect, βj is the jth level whole-plot treatment effect, (αβ)ij is one of the ab interaction effects. The μ, αi, βj and (αβ)ij are all constants such that for all i, j
Furthermore, the γk(i) are the whole-plot errors which are independently and normally distributed with the same variance and zero mean, i.e. γk(i) ∼ N(0,σW), while the εijk are the split-plot errors which are independently and normally distributed with the same variance and zero mean, i.e. εijk ∼ N(0,σ). If there are c replications, then there are ac γk(i) terms and abc εijk terms.
If we use the three fixed factor ANOVA from Anova with more than Two Factors as a guide with factor C playing the role of the replications, then the Split-Plot Anova table takes the form:
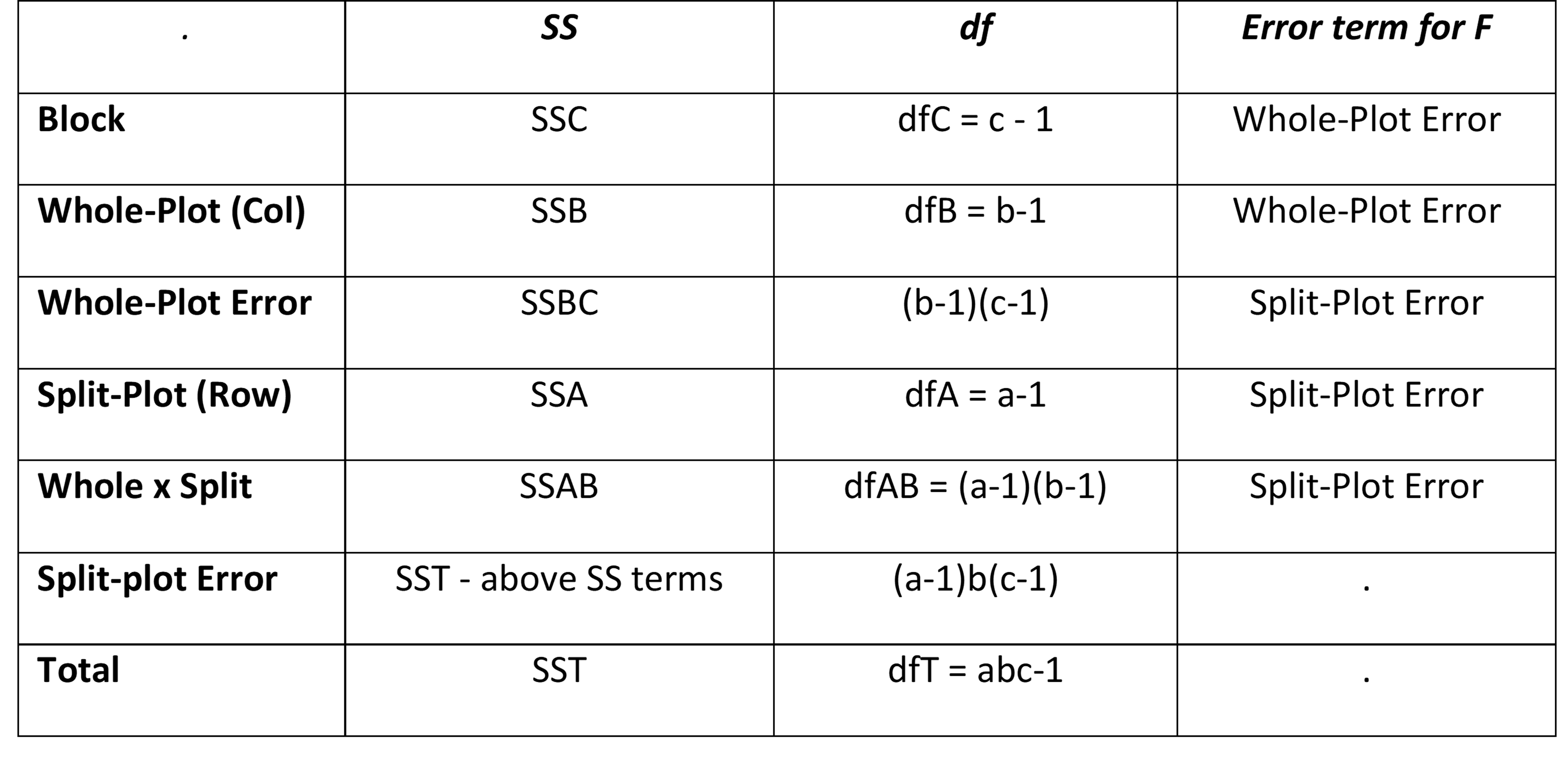
The model for a split-plot design where the main plots follow an RCB design is
This time, the γk terms serve as the blocking effect, while the whole plot error variance 
The RCB split-plot design takes the form:
Great content! Thanks for sharing. I have a question out of curiosity. I did a split-plot experiment with the RCB model (whole plot factor A with 2 levels, split plot factor B with 4 levels and 3 blocks). On my ANOVA I got p=0.03 on the Error 1 column (A x Block interaction) and no effect neither on the whole (p=0.08) nor split plot (p=0.24) factors. While I don’t know if I should be concerned on the significance of the Error 1; I run the same data assuming CRD model with 3 replications out of curiosity and got the same Error 1 p<0.05 but now the whole factor is significant (p=0.03). I know I must stay on my initial RCB design, but what is happening? why the same data set returns different effects when analyzed with CRD model?
Hi Kevin,
Statistics is partially mathematics and partially art. Often more than one statistical test is available to address a problem, and often these tests give different results. There are many reasons for this, including:
1. Often the assumptions are different, and so you should choose the test that best meets the assumptions
2. Since statistics is probabilistic, sometimes one test has less type I error but more type II error
3. Fortunately, very often different tests, even using different assumptions, yield fairly similar results. But this isn’t always the case.
4. Sometimes the design is correct but one of the chosen test’s assumptions is violated during the execution of the experiment
For your analysis, you are choosing between RCB and CRD. In general, CRD is the preferred test (more accurate results), but often the resources aren’t available to perform CRD and so RCB is chosen.
If you were able to perform CRD, why did you choose to use RCB?
If multiple tests are available, then, as you have recognized, it is a bad idea to pick the result, a posteriori, that you prefer. Since this was not your intention, I would be tempted to present both results accompanied by an open explanation (although this might not be accepted by some journals and other organizations).
Charles
Can we still analyze a field trial as a split plot design if the main plots are not randomized and subplots are randomized? I have had a random factor with block*main plot to address the error caused due to randomization. Does anyone have a proper reference to this thing if it is applicable?
Sorry, but I don’t have an answer to your question.
Charles
Hiii Charles thank you for your support and encouragement
I want to determine optimum rate of phosphorus fertilizer rate and irrigation level for maize .can I use split plot design ?please help me by giving direction and send me materials which are important for this study.
With best regards
Hello Shishay,
Thank you for your kind remarks.
Whether a split plot design is best depends on many factors, including limitations that you may have in terms of resources (time, expenses, etc.) You should read the tutorial at
https://real-statistics.com/design-of-experiments/
Charles
How to calculate degree of freedom
If factor A = Nitrogen having 4 levels and phosphorus having 3 levels
Replicated three times
Design RCB split plot
Email me the answer
Sorry, Siddique, but I don’t understand your design.
Charles
Hi Charles thank you for this great website. I’m faced with a little experimental layout problem in which we want to test the impact of different rates of Chromium on plant growth with different rates of organic amendments and different types of amendments. I would use a split-plot design, where the different types of amendments are the whole plots, and within each whole plot, the amendment rate and Cr rate can be fully randomised. I’m not interested how the various amendments interact with each other. Is the split-plot design a valid approach for this problem?
Derk,
A split-ploy design might be suitable. It depends on the details, especially the limitation you have when conducting the experiment.
Charles
Hi Charles,
I’ve made a trial in which I have tried 2 different irrigation volumes and 4 types of irrigation schedules to determine plant productivity with a specific crop. I’ve used 8 growing benches (4 in one unit and another 4 in other unit), each treatment was repeated twice. I’m not sure if I should use a split plot design test or a simple 2-way ANOVA test. What would you recommend?
Congratulations for this useful website.
Regards,
Ricardo
Ricardo,
What to do depends on the following:
(1) What hypothesis or hypotheses do you wish to test?
(2) What is the relationship between the irrigation volumes, irrigation schedules, units and benches?
Charles
The hypotheses are: Is yield affected by 1)irrigation volumes/2)irrigation schedules/3)both?
For instance: for a given amount of water (let’s say 20L) I’ve distributed these same 20L in 4 different ways (irrigation schedules). I called unit to a stack with four growing benches. The 2 units are side by side. In one unit I used 20L, in the other unit I used 40L. The 4 different irrigation schedules were replicated in both units. Is this clearer now?
Ricardo,
I understand that you have
(a) 2 irrigation volumes (20L and 40L)
(b) 4 irrigation schedules
(c) 8 growing benches: 4 for the 20L (presumably one per schedule type) and 4 for the 40L (also presumably one per schedule type)
(d) 2 replications
From (a) and (b), I understand that you have 2 x 4 = 8 combinations. Since there are 2 replications (from d), does this means that you have a sample of size 2 x 8 = 16?
If I ignore the bench factor, then you can use two-fixed-factor ANOVA for your analysis (with 2 replications). This approach would not take into account Bench as a confounding factor.
Since there are 2 replications if I assume that all 8 of the 20L samples are done on bench 1 and all 8 of the 40L samples are done on bench 2, then I won’t be able to take the effect of Bench into account. If instead, I assume that for the first replication, the 4 20L samples are done on bench 1 and the 4 40L samples are done on bench 2, but for the second set of replications the 4 20L samples are done on bench 2 and the 4 40L samples are done on bench 1, then I can take the Bench factor into account. In this case, I can use three-factor ANOVA (with no replications). I could use instead split-plot design if I randomize the allocation of the 20L/40L and schedules A/B/C/D randomly as described on this webpage.
Charles
Hi Charles,
I think I got it then. It’s mostly appropriate to use a 2-way ANOVA instead of the Split Plot design, since I could not randomize the irrigation volumes and the schedules.
Thanks for you support,
Ricardo
Thank about this information
I can’t add (real statistics using excel) to Data analysis function by steps: file.. options.. add-in.
(also I used browser not see real statistics as function to add it)
I need some help
With Best Regards
Fadhil,
Sorry, but I don’t understand your question. Perhaps the following webpage will be helpful:
https://www.real-statistics.com/appendix/faqs/disappearing-addins-ribbon/
Also, make sure that the software has been installed properly. You can determine this when the formula =VER() works properly.
Charles
Hi Charles! Congrats for the site, it’s really awesome and helpful!
I’m in doubt if I should analyze my dataset as split-plot or repeated measures. I have 2 water management levels (irrigated and rainfed) and 2 sugarcane cultivars during 2 crop seasons. My variables are stalk, sugar, and cumulative root density (CRD), which is analyzed in 4 soil depths (CRD1-CRD4). To solve this problem I considered irrigation levels as plots and cultivars as subplots (split-plot design) but I’d like to know if there is and what is the effect of crop season over these variables. In this case, I have to make a unique analysis, but I can’t make it at all.
I don’t quite understand the scenario that you are describing. First of all, what hypothesis are you trying to test?
Charles
Hi Charles!
The hypotheses are:
1. Does irrigation affect the root distribution pattern along with the soil profile?
2. Does the root distribution pattern have any correlation with yield (stalk and sugar)?
3. If these two hypotheses are true, how it occurs in cane-plant (1st crop season) and first ratoon (2nd crop season)?
These sorts of hypotheses seem to go beyond those that can be tested via the techniques that you are trying to explore.
Sorry, but I am unable to help you.
Charles
Hi Charles!
Now I’m ‘just a little’ concerned…
Are you saying that for testing those hypotheses I should use a multivariate analysis?
Any other suggestions?
Thank you!
Hello,
I don’t know what specific approaches to use.
Charles
Hello Charles!
I apologize for being careless…the hypotheses to be tested are:
1. The water management (irrigated or rainfed) influences the yield and root distribution pattern down the soil profile.
2. There is a cultivar with a higher yield (stalk/sugar) and best quality (fibre/purity) than other under irrigation.
3. The age of the cane (crop season) has influence over root distribution pattern and yield.
Regards,
As mentioned in my previous response, I don’t know how to perform a single analysis to address the hypotheses you are trying to test. It seems to me that these are separate analyses. In fact, each of your three points may involve multiple analyses. If it is necessary to perform multiple analyses, you will need to use some sort of familywise error correction (Bonferroni?).
Charles
To test those hypotheses I’ve carried a study with 2 water management (irrigated and rainfed) and 2 cultivars, with 6 replications. It lasted for 2 crop seasons and the roots were analyzed in 4 soil layers (0-20, 20-40, 40-60 and 60-80 cm). The response variables are stalk, sugar, fibre, purity, cumulative root density and root diameter (for each layer).