We now show the first of two methods for dealing with missing data in a randomized complete block design. This method can be used where one cell is missing. There are extensions to this method to handle more than one missing data element, but we won’t consider them here since the second method, using regression, handles these more easily.
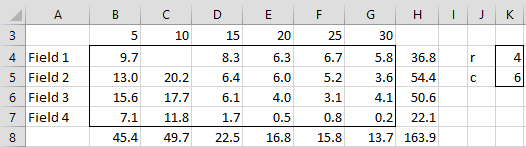
Example 1: Repeat Example 1 of Randomized Complete Block Design with the data in Figure 1.
Figure 1 – RCBD with missing data
Here cell C4 is missing. We start by imputing a value for this cell as follows.
Let r = # of rows (blocking factor) and c = # of columns (treatment factor). Let xij be the value of the cell in the ith row and jth column. Let xi. = the sum of the values in the ith row, x.j = the sum of the values in the jth column and x.. = the sum of all the values. Then the missing value can be replaced by the following least-squares estimate:
For Example 1
This can be calculated in Excel by the formula =(H4*K4+C8*K5-H8)/((K4-1)*(K5-1)).
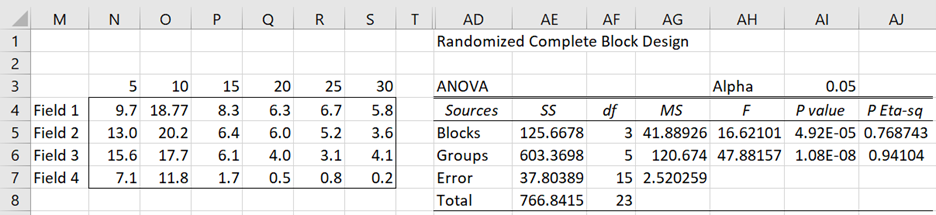
We now create the RCBD analysis (as shown on the right side of Figure 2) using the Randomized Complete Block Anova data analysis tool based on the data in Figure 1 with cell D5 filled in with the value 7.46 (as shown on the left side of Figure 2).
Figure 2 – Initial RCBD analysis
We next need to make the following modifications:
- Reduce the total degrees of freedom, dfT (cell AF8) by 1 (since one data element is missing). This, in turn, will reduce the error degrees of freedom, dfE (cell AF7) by 1.
- Reduce the Blocks SS (SSRows) and Groups SS (SSCols) as follows:
where xij is the estimate of the missing data element.
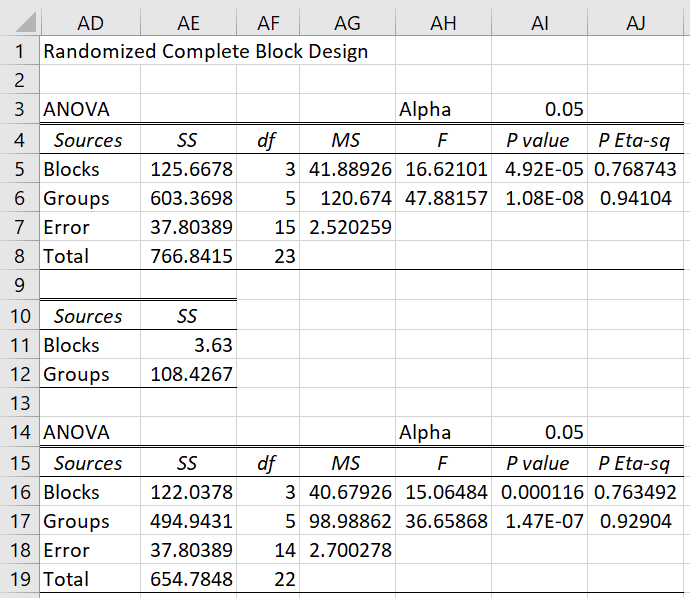
Figure 3 – Adjusted RCBD
Here, cell AE11 contains the formula =(C8-(K4-1)*O4)^2/(K4*(K4-1)) and cell AE16 contains =AE5-AE11. Similarly, cell AE12 contains =(H4-(K5-1)*O4)^2/(K5*(K5-1)) and cell AE17 contains =AE6-AE12.