2^k Factorial Design w/o Replications

Basic Concepts

For designs without replications, we need to pool some of the interaction factors into the error term. We have a number of choices for how we do this, but we avoid including interaction factors in the error whose effect size are outliers since this will inflate the MSE value. We can use any of the techniques described on the rest of this website to determine which factors are outliers (i.e. their effect size is an outlier compared to the effect sizes of all the factors).

Example

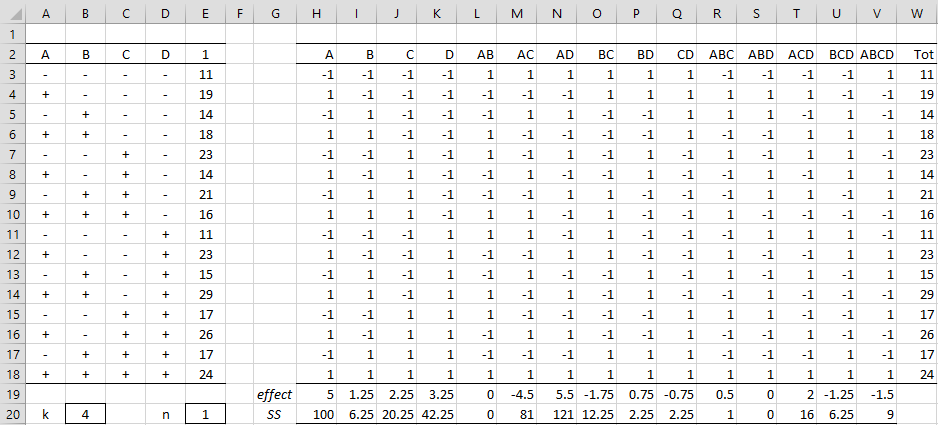
Example 1: Create the 2^4 factorial design for the data in range A2:E18 of Figure 1.

Figure 1 – Design without Replications

We construct the effect size and SS values exactly as we did for Example 1 of 2^k Factorial Design Basic Concepts. These values are shown in range H19:V20 of Figure 1.

We pool the 3^rd and 4^th order interaction factors to make up the error term. Note that the extreme values for the effect sizes are 5.5 (AD) and -4.5 (AC). None of the 3^rd and 4^th order interaction factors have effect sizes anywhere near these extreme values and so we don’t need to worry about inflating the MSE value (in fact, if we use the Box Plot with Outliers, Grubbs’ Test or Outliers and Missing Data options of the Descriptive Statistics and Normality Test data analysis tool, we will see that no potential outliers are flagged).

ANOVA

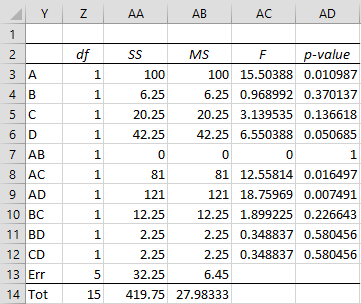
Constructing the ANOVA table as we did for Example 1 in 2^k Factorial Design Basic Concepts, we get the analysis shown in Figure 2.

Figure 2 – Design without Replications (design 1)

We see that factors A, AC, AD are significant and D is borderline.

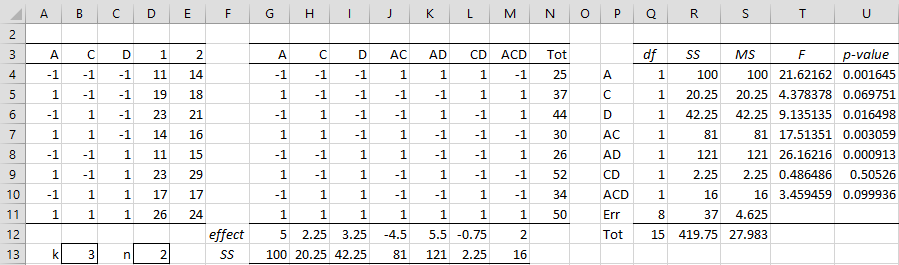
Note that no factor containing B is significant and so another approach is to eliminate factor B from the analysis. This is equivalent to a 2^3 factorial design with n = 2 replications (e.g. A = +, C = +, D = – has replications 14 and 16). The analysis for this design is shown in Figure 3.

Figure 3 – Reduced design (design 2)

This time, factors A, D, AC, and AD are significant.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

PennState (2017) Unreplicated 2^k factorial design
https://online.stat.psu.edu/stat503/lesson/6/6.3

Montgomery, D. C. (2012) The 2^k factorial design. Design and analysis of experiments, 8th ed.
https://faculty.ksu.edu.sa/sites/default/files/douglas_c._montgomery-design_and_analysis_of_experiments-wiley_2012_edition_8.pdf