2^k Factorial Design Tool

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack contains the following array functions.

Design2k(k, lab, d): returns a 2^k design including d-way interactions (d = 0, 2, 3; default = 2); output contains 2^k rows when lab = FALSE (default) and k columns if d = 0 or d + C(k,2) columns if d = 2 or d + C(k,2) + C(k,3) columns if d = 3; values consist of only -1 and +1; if lab = TRUE then an extra row of labels is appended to the output.

ExpandDesign2k(R1, d): returns a 2^k design with headings, including d-way interactions (d = 2, 3; default = 2); output is the same as Design2k(k, TRUE, d), except that the first k columns consist of the values in range R1 (which contains only values 1 and -1, without headings).

Effect2k(R1, R2, lab, d): returns a column array consisting of the effect size values for the design described by R1 and R2, where R1 contains the +1 and +1 values (such as range A4:C11 of Figure 1 and R2 contains the data values (such as range D4:G11 of Figure 1); if lab = TRUE (default FALSE), then an extra column is appended with factor labels.

SS2k(R1, R2, lab, d): returns an array consisting of the SS values for the design defined by R1 and R2, exactly as for Effect2k except that SS values are output instead of effect sizes.

Data Analysis Tool

Real Statistics Data Analysis Tool: The Real Statistics Resource Pack provides the 2^k Factorial Design data analysis tool which automates the steps described above. We show how to use this tool for Example 1 of 2^k Factorial Design Basic Concepts.

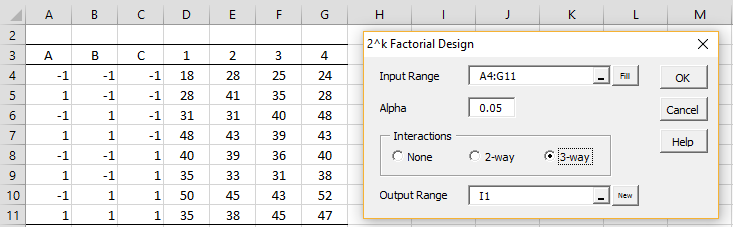
Press Ctrl-m (or an equivalent) and choose the ANOVA option from the original interface or the Anova tab from the multipage interface. Now choose the 2^k Factorial Design option and fill in the dialog box that appears as shown in Figure 1. Note that the row headings are not included in the Input Range.

2^k design dialog box

Figure 1 – 2^k Factorial Design dialog box

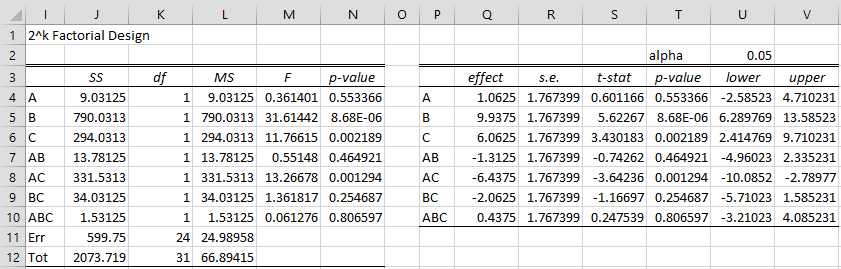
Upon pressing the OK button the output in Figure 2 is displayed.

2^k design analysis tool

Figure 2 – 2^k Factorial Design data analysis tool

Note that if you had inserted the range A4:D11 in the Input Range in Figure 1 (and so there would only be one column of data), you couldn’t select the 3-way Interaction option, since this would force the error terms (in cells J11 and K11) to be zero.

Range I4:J12 of Figure 2 contains the array formula =SS2k(A4:C11,D4:G11,TRUE,3). Similarly, range P4:Q10 contains the array formula =Effect2k(A4:C11,D4:G11,TRUE,3).

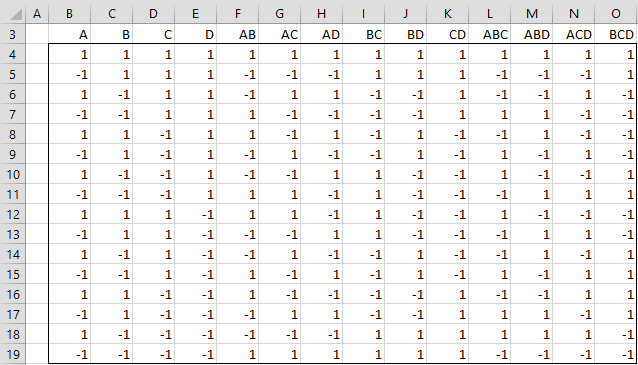
If instead of entering a range in the Input Range, you enter an integer between 2 and 20, then a design table would be output instead. E.g. if you enter the integer 4 in the Input Range and select the 3-way option for the Interactions, the output is as shown in Figure 3.

2^4 design

Figure 3 – 2^4 Design

Note that range B3:O19 contains the array formula =Design2k(4,TRUE,3). Finally, note that the output from the formula =ExpandDesign2k(A4:C11,2) where the range A4:C11 is as shown in Figure 4.

ExpandDesign2k function

Figure 4 – ExpandDesign2k formula

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

PennState (2017) The 2k factorial design
https://online.stat.psu.edu/stat503/lesson/6

Montgomery, D. C. (2012) The 2k factorial design. Design and analysis of experiments, 8th ed.
https://faculty.ksu.edu.sa/sites/default/files/douglas_c._montgomery-design_and_analysis_of_experiments-wiley_2012_edition_8.pdf

28 thoughts on “2^k Factorial Design Tool”

  1. Hello! I have some trouble trying to make an analysis with 5 factor and 3 datasets. If I eliminate one factor (leaving 4 factors and 3 datasets) it works really well. Is there a reason for this? I think it’s possible to solve this since it’s a workbook problem, but cannot add this extra factor to make it work.

    Reply

    • Hello Daniel,
      I just tried it and it seemed to work for me, but I may not have tried the same situation as you.
      Did you include 2-way or 3-way interactions?
      Can you you email me an Excel spreadsheet with your data and results?
      Charles

      Reply

  2. hello,

    I can’t use 2^k Factorial Design because each time it gives me an error that I can’t have negative numbers in the input range. But I’m using your table that you gave as an example. what should I do?

    thank you

    Reply

  5. Good morning Charles

    I design an experiment in which there will be 3 variables. Due to the non-linear behavior of the process, I need to introduce a central point between the minimum and maximum. How can I do it in real statistic? How to code variables. I know that min = -1, max = 1, but what about the value in the middle?

    Reply

Leave a Comment