Basic Concepts
The Harrell-Davis quantile is an approach for providing a more robust estimate of percentiles and related measures such as the median. These can be useful, for example, with bimodal data.
Given a data set {x1, …, xn} with x1 ≤ x2 ≤ … ≤ xn, and 0 ≤ p ≤ 1, the pth Harrell-Davis quantile is defined as
where
The Harrell-Davis median is the Harrell-Davis quantile where p = .5.
The Harrell-Davis MAD is then defined as
where x-tilde is the Harrell-Davis median of the xi.
Worksheet Functions
Real Statistics Function: The Real Statistics Resource Pack supplies the following functions.
HD_QUANTILE(R1, p) = pth Harrell-Davis quantile for the data in the column array R1.
You can calculate the Harrell-Davis median via the formula =HD_QUANTILE(R1,.5).
The Harrell-Davis version of the MAD can be calculated via the formula MAD(R1,TRUE).
Example
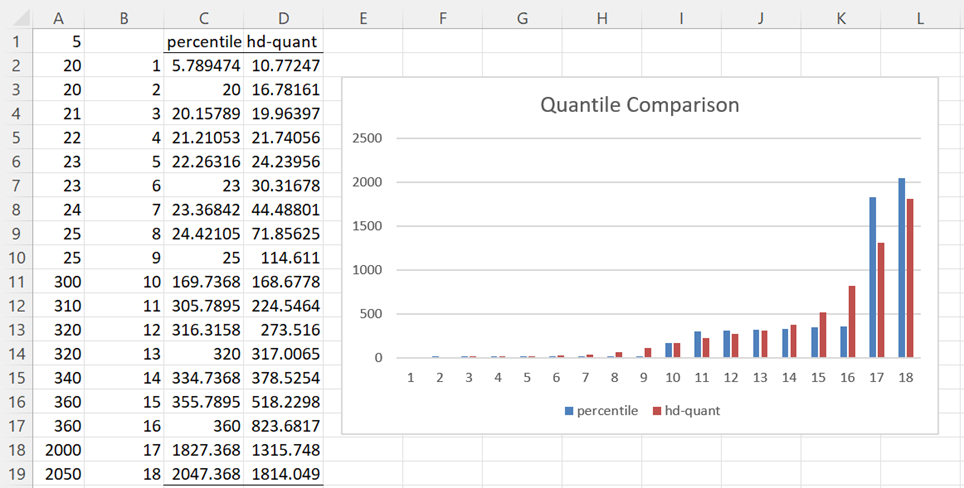
Example 1: Compare the usual percentile measures with the Harrell-Davis quantiles for the data in column A of Figure 1.
Figure 1 – Quantile comparison
The results are shown on the right side of Figure 1. E.g. cell B2 contains the worksheet formula =PERCENTILE_EXC(A1:A19,K2/19) and cell C2 contains =HD_QUANTILE(A1:A19,B2/19). The Harrell-Davis metric seems to smooth out the quantile measures.
Observation
For a wide range of distributions (and samples from these distributions), the Harrell-Davis quantiles provide a more faithful estimate of the population quantiles than the usual sample-based quantile estimates such as PERCENTILE.INC and PERCENTILE.EXC (see Ranking Functions in Excel).
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Akinshin, A. (2020) DoubleMAD outlier detector based on the Harrell-Davis quantile estimator
https://aakinshin.net/posts/harrell-davis-double-mad-outlier-detector/#Rosenmai2013
Akinshin, A. (2021) Efficiency of the Harrell-Davis quantile estimator
https://aakinshin.net/posts/hdqe-efficiency/
Dear Charles,
I think, that HD-MAD can be used similarly to standard MAD for identifying the outliers. Does it mean, that the same constants can be used?
Median ± 2.5*1.4826*MAD (or 3*1.4826)
analogously:
HD-Median ± 2.5*1.4826*HD-MAD (or 3*1.4826).
Am I right?
Thank you, best regards,
Martin
Dear Charles,
it works nice! HD_QUANTILE returns more smooth quantiles. It will help with data with problematic distribution.
The function HD_MAD seems not to be incorporated in version 7.10.
Best regards, Martin
Martin,
I made an error in the announcement of Rel 7.10. The HD version of MAD is not in a separate function, it is an option of the existing MAD function. The new version is MAD(R1, harrell) where R1 contains the data and if harrell = TRUE, then the Harrell-Davis version of the median is used when calculating the MAD, while if harrell = FALSE (default), then the ordinary version of the MAD is returned.
Charles