Basic Concepts
Excel Functions: Figure 1 summarizes the various ranking functions available in all versions of Excel for a data set R1. We describe each of these functions in more detail on the rest of this webpage, plus we describe additional ranking functions that are only available in versions of Excel starting with Excel 2010.
Figure 1 – Ranking functions in Excel
All these functions ignore any empty cells and cells with non-numeric values.
MIN and MAX
Definition 1: MIN(R1) = the smallest value in R1 and MAX(R1) = the largest value in R1
Example 1: For range R1 with data elements {4, 0, -1, 7, 5}
- MIN(R) = -1
- MAX(R) = 7
SMALL and LARGE
Definition 2: SMALL(R1, n) = nth smallest value in R1 and LARGE(R1, n) = nth largest value in R1. Here n can take on any value from 1 to the number of elements in R1, i.e. COUNT(R1).
Observation:
SMALL(R1, n) = LARGE(R1, COUNT(R1) – n + 1)
LARGE(R1, n) = SMALL(R1, COUNT(R1) – n + 1)
Example 2: For range R1 with data elements {4, 0, -1, 7, 5}
- LARGE(R1, 1) = 7, LARGE(R1, 2) = 5, LARGE(R1, 5) = -1
- SMALL(R1, 1) = -1, SMALL(R1, 2) = 0, SMALL(R1, 5) = 7
Real Statistics Function: The Real Statistics Resource provides the following worksheet function.
SMALLExact(R1, k, prec): When k is an integer, this function is equivalent to SMALL(R1,k). Otherwise, it takes the interpolated value =SMALL(R1,INT(k))+(k-INT(k))*(SMALL(R1,INT(k)+1)-SMALL(R1,INT(k)))
Values of k in the range 1-prec ≤ k < 1 are treated like k = 1 and any k in the range n < k ≤ n+prec, where n = the number of elements in R1, is treated like k = n. prec defaults to 0.
RANK
Definition 3: RANK(c, R1, d) = the rank of data element c in R1. If d = 0 (or is omitted) then the ranking is in decreasing order, i.e. a rank of 1 represents the largest data element in R1. If d ≠ 0 then the ranking is in increasing order and so a rank of 1 represents the smallest element in R1.
Example 3: For range R1 with data elements {4, 0, -1, 7, 5}
- RANK(7, R1) = RANK(7, R1, 0) = 1
- RANK(7, R1, 1) = 5
- RANK(0, R1) = RANK(0, R1, 0) = 4
- RANK(0, R1, 1) = 2
Observations
- If LARGE(R1, n) = c then RANK(c, R1) = RANK(c, R1, 0) = n
- If SMALLR1, n) = c then RANK(c, R, 1) = n
- RANK(c, R1) + RANK(c, R1, 1) = COUNT(R1) + 1
- For any values c and d, 1 ≤ RANK(c, R1, d) ≤ COUNT(R1)
Excel’s RANK function does not take care of ties very well. E.g., if the range R1 contains the values {1, 5, 5, 0, 8}, then RANK(5, R1) = 2 because 5 is the 2nd highest ranking element in range R. But 5 is also the 3rd highest ranking element in the range, and so for many applications, it is useful to consider the ranking to be 2.5, namely the average of 2 and 3.
To correct for ties for any data element c in the range R1, you can use the following formula (see Built-in Excel Functions for a description of the COUNTIF function):
= RANK(c, R1) + (COUNTIF(R1, c) – 1) / 2
Excel Worksheet Functions
Excel addresses this issue by providing the function RANK.AVG, which takes the same arguments as RANK but returns the average of equal ranks as described above. Excel also provides the function RANK.EQ, which is equivalent to RANK.
While the RANK function is available in all releases of Excel, the RANK.AVG and RANK.EQ functions are not available in releases prior to Excel 2010.
If the range R1 contains the values {1, 5, 5, 0, 8}, then RANK.AVG(5, R1) = 2.5, while if R1 contains the values {1, 5, 5, 8, 5}, then RANK.AVG(5, R1) = 3, i.e. the average of 2, 3, and 4.
Real Statistics Functions
For users of versions of Excel prior to Excel 2010, the Real Statistics Resource Pack provides the function RANK_AVG which is equivalent to RANK.AVG. In fact, as explained below, RANK_AVG has some advantages over RANK.AVG even for users of newer versions of Excel.
RANK_AVG(x, R1, order, num_digits) = the ranking of x in range R1, where x, as well as any numeric entries in R1, are rounded off to num_digits decimal places; when there are ties, the average ranking is used. If num_digits is omitted then it defaults to 8. If order = 0 (or is omitted) then the ranking is in decreasing order, while if order ≠ 0 then the ranking is in increasing order.
The Real Statistics Resource Pack also supplies the following related array functions:
RANKS(R1, order, num_digits): returns a column array with the values RANK_AVG(x, R1, order, num_digits) for each numeric element x in R1. Entries for non-numeric elements are not included in the list.
RANKCOL(R1, order, num_digits): returns an array of the same size and shape as R1, each column of which contains the ranks for that column (the data in each column is ranked separately).
Example 4: Using the RANK.AVG or RANK_AVG function, find the ranks of the data in range E17:E23 of Figure 2.
Figure 2 – Average ranking
The result is shown in column F of Figure 2. For example, the average rank of 8 (cell E21 or E22) is 1.5, as calculated using the formula =RANK_AVG(E21,E17:E23) or =RANK.AVG(E21,E17:E23) as shown in cell F21 (or F22). If instead, you want the ranking in the reverse order (where the lowest value gets rank 1) then the results are shown in column G. This time using either =RANK_AVG(E21,E17:E23,1) or =RANK_AVG(E21,E17:E23,1) we see that the rank of 8 is 6.5 as shown in cell G21.
Cautions
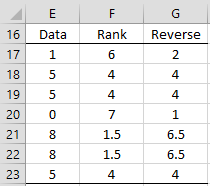
There are several flaws in the RANK, RANK.EQ and RANK.AVG functions. E.g. in Figure 3, we show two samples of data in columns A and B, with the differences shown in column D (e.g. cell D4 contains the formula =A4-B4).
Note that three cells (D5, D8, and D13) all have the value 5.5. Thus, we would expect that the rankings for each would be the same. In fact, we see that cell E5 contains the value 5 based on the formula =RANK.AVG(D5,D4:D13), while cells E8 and E13 contain the ranking 6.5. The ranking in all three cells should actually be 6. The reason for this is that apparently, the RANK.AVG function treats the value in cell D5 as slightly higher than 5.5. This produces unpredictable results.
Note too that cell E4, which contains the formula =RANK.AVG(D4,D4:D13), has the correct value, namely 1, but the formula =RANK.AVG(12.4,D4:D13) yields the error value #N/A. This means that the RANK.AVG function does not recognize 12.4 as one of the values in range D4:D13, since it doesn’t recognize the value in cell D4 as being 12.4.
Figure 3 – RANK.AVG vs. RANK_AVG
Note too that the RANK, RANK.EQ and RANK.AVG functions only take a cell range as their second argument. Thus, you can’t use an array formula such as =RANK.AVG(A4,A4:A13-B4:B13). Although A4:A13-B4:B13 evaluates to an array, it can’t be used as an argument in RANK.AVG. The Real Statistics array formula =RANK_AVG(A4,A4:A13-B4:B13), however, is valid. Keep in mind that this is an array formula, and so you must press Ctrl-Shft-Enter (unless you are using Excel 365).
In fact, you can also insert the array formula =RANK_AVG(D4:D13,D4:D13) in range F4:F13 to get the same result shown in Figure 3.
Data Analysis Tool
Excel Data Analysis Tool: In addition to the functions described above, Excel also provides a Rank and Percentile data analysis tool. This tool uses the Excel 2007 definitions of rank and percentile, i.e. those used by the RANK and PERCENTILE functions.
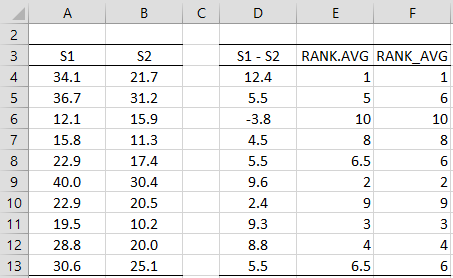
Example 5: Calculate the rank and percentile for the data in Figure 4 using Excel’s Rank and Percentile data analysis tool.
Figure 4 – Score data
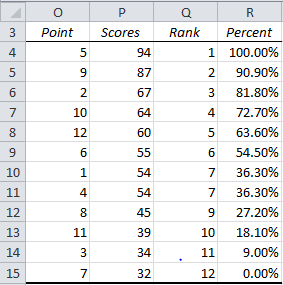
For the data in Figure 4, the data analysis tool generates the output shown in Figure 5.
Figure 5 – Rank and Percentile data analysis tool
The table is sorted in rank order. Point indicates the index of the corresponding score in the input data range. E.g. 94 (cell P4) is the 5th data element in the input range but is the largest data element and so has rank 1.
PERCENTILE
Definition 4: For any percentage p, i.e. a value such that 0 ≤ p ≤ 1 or equivalently 0% ≤ p ≤ 100%, the worksheet function PERCENTILE(R1, p) = the element at the pth percentile.
If p(n–1) = k for some integer value k = 0, 1, 2, … n–1 where n = COUNT(R), then PERCENTILE(R1, p) = SMALL(R1, k+1) = the k+1th element in R1. If p(n-1) is not an integer, then the PERCENTILE function performs a linear interpolation as described in the examples below.
Example 6: For range R1 with data elements {4, 0, -1, 7, 5}, the 5 data elements in R1 divide the range into 4 intervals of size 25%, i.e. 1/(5-1) = .25. Thus
- PERCENTILE(R1, 0) = -1 (the smallest element in R1)
- PERCENTILE(R1, .25) = 0 (the second smallest element in R1)
- PERCENTILE(R1, .5) = 4 (the third smallest element in R1)
- PERCENTILE(R1, .75) = 5 (the fourth smallest element in R1)
- PERCENTILE(R1, 1) = 7 (the fifth smallest element in R1)
For other values of p we need to interpolate. For example
- PERCENTILE(R1, .45) = 0 + (4 – 0) * (0.45 – 0.25) / (.5 – 0.25) = 3.2
- PERCENTILE(R1, .80) = 5 + (7 – 5) * (0.8 – 0.75) / (1.0 – 0.75) = 5.4
Of course, Excel’s PERCENTILE function calculates all these values automatically without you having to figure things out.
Excel Worksheet Functions
Releases of Excel after Excel 2007 provide two versions of the percentile function: PERCENTILE.INC and PERCENTILE.EXC. The first of these is called the inclusive version since 0 ≤ p ≤ 1, and is equivalent to PERCENTILE. The second of these is called the exclusive version of the percentile function since 0 < p < 1.
If n = COUNT(R1), then for any integer k with 1 ≤ k ≤ n,
PERCENTILE.EXC(R1, k/(n+1)) = SMALL(R1, k), i.e. the kth smallest element in R1
For 0 < p < 1, if p(n+1) is not an integer, then PERCENTILE.EXC(R1, p) is calculated by linear interpolation between the corresponding values in R1. For p < 1/(n+1) or p > n/(n+1), no interpolation is possible, and so PERCENTILE.EXC(R1, p) returns an error value.
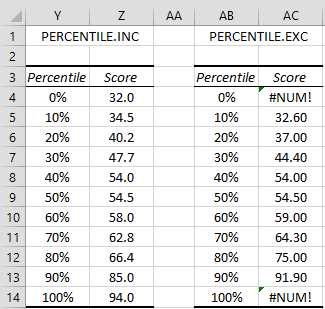
Example 7: Find the 0 – 100 percentiles in increments of 10% for the data in Figure 4 using both PERCENTILE.INC and PERCENTILE.EXC.
The result is shown in Figure 6. E.g. the score at the 60th percentile is 58 (cell Z10) using the formula =PERCENTILE.INC(B3:M3,Y10), while it is 59 (cell AC10) using the formula =PERCENTILE.EXC(B3:M3,AB10).
Figure 6 – PERCENTILE.INC vs. PERCENTILE.EXC
Real Statistics Function
The Real Statistics Resource Pack contains the following function which calculates the pth percentile (0 ≤ p ≤ 1) based on range R1 with n elements using one of the Hyndman-Fan definitions of percentile as determined by argument m.
PERCENTILE_EXC(R1, p, m) = xh′ + (xh′+1 – xh′)(h – h′)
where h′ = INT(h) and h is defined as follows
h = np if m = 4
h = np + .5 if m = 5
h = (n+1)p if m = 6 (default)
h = (n–1)p + 1 if m = 7
h = (n+1/3)p + 1/3 if m = 8
although if this calculation results in a value smaller than the smallest value in R1 or larger than the largest value in R1, then PERCENTILE_EXC(R1, p, m) = MIN(R1) or = MAX(R1), respectively, instead of the values defined above.
PERCENTILE_EXC also supports the discontinuous Hyndman-Fan versions of percentile (where m = 1, 2, or 3).
For users of versions of Excel before Excel 2010, PERCENTILE_EXC can be used in place of PERCENTILE.EXC; in fact, PERCENTILE_EXC(R1, p) = PERCENTILE.EXC(R1, p) except when PERCENTILE_EXC(R1, p) takes an error value, in which case, PERCENTILE_EXC(R1, p) takes the value MIN(R1) or MAX(R1).
Note too that PERCENTILE_EXC(R1, p, 7) = PERCENTILE(R1, p).
Weighted Percentiles
Click here for information about weighted percentiles.
Harrell-Davis Quantiles
Another approach to calculating the percentile based on a sample is given by the Harrell-Davis Quantile. Click here for more information about this statistic.
PERCENTRANK
Definition 5: PERCENTRANK(R1, c) = the percentile of data elements in R1 up to c. Thus, if PERCENTRANK(R1, c) = p then PERCENTILE(R1, p) = c.
Example 8: For range R1 with data elements {4, 0, -1, 7, 5}
- PERCENTRANK(R1, 5) = .75
- PERCENTRANK(R1, 5.4) = .8
For any value c in the range R1, you can calculate PERCENTRANK(R1, c) as the number of elements in R1 less than c divided by the number of elements in R1 less 1. Since R1 contains 5 elements of which 3 elements are less than 5 (namely -1, 0, and 4), we know that PERCENTRANK(R1, 5) = 3/(5-1) = .75.
Similarly, we see that PERCENTRANK(R1, 7) = 4/(5-1) = 1. Since 5.4 is not in range R1 but is between the elements 5 and 7 in R1, the formula PERCENTRANK(R1, 5.4) is calculated as a linear interpolation between .75 and 1, namely
Observation: You can also add a third argument that represents the number of significant figures in the answer. Thus PERCENTRANK(R1, .85, 5) = .30312.
Excel Worksheet Functions
Releases of Excel after Excel 2007 provide two versions of the percent rank function: PERCENTRANK.INC and PERCENTRANK.EXC. The first of these is equivalent to PERCENTRANK and the second is defined so that if PERCENTRANK.EXC(R1, c) = p then PERCENTILE.EXC(R1, p) = c.
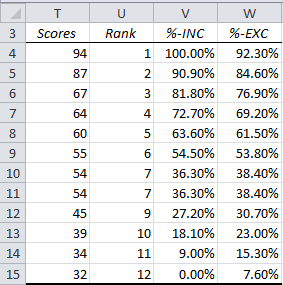
Example 9: Repeat Example 5 using the PERCENTRANK.INC and PERCENTRANK.EXC functions.
The result is shown in Figure 7. E.g. the score 45 (cell T12) is at the 27.2th percentile (cell V12) using the formula =PERCENTRANK.INC(T4:T15,T12), while it is at the 30.7th percentile (cell W12) using the formula =PERCENTRANK.EXC(T4:T15,T12).
Figure 7 – PERCENTRANK vs. PERCENTRANK.EXC
QUARTILE
Definition 6: For any integer k = 0, 1, 2, 3, or 4, QUARTILE(R1, k) = PERCENTILE(R1, k/4). If c is not an integer, but 0 ≤ c ≤ 4, then QUARTILE(R1, c) = QUARTILE(R1, INT(c)).
Observation:
- QUARTILE(R1, 0) = PERCENTILE(R1, 0) = MIN(R1)
- QUARTILE(R1, 1) = PERCENTILE(R1, .25)
- QUARTILE(R1, 2) = PERCENTILE(R1, .5) = MEDIAN(R1)
- QUARTILE(R1, 3) = PERCENTILE(R1, .75)
- QUARTILE(R1, 4) = PERCENTILE(R1, 1) = MAX(R1)
Example 10: For range R1 with data elements {4, 0, -1, 7, 5}
- QUARTILE(R1, 0) = PERCENTILE(R1, 0) = -1
- QUARTILE(R1, 1) = PERCENTILE(R1, .25) = 0
- QUARTILE(R1, 2) = PERCENTILE(R1, .5) = 4
- QUARTILE(R1, 3) = PERCENTILE(R1, .75) = 5
- QUARTILE(R1, 4) = PERCENTILE(R1, 1) = 7
Excel Worksheet Functions
Releases of Excel after Excel 2007 provide two versions of the quartile function: QUARTILE.INC and QUARTILE.EXC. The first of these is equivalent to QUARTILE and the second is defined so that QUARTILE.EXC(R1, k) = PERCENTILE.EXC(R1, k/4).
Real Statistics Function
The Real Statistics Resource Pack provides the following worksheet function.
QUARTILE_EXC(R1, k, m) = PERCENTILE_EXC(R, k/4, m)
m takes integer values between 1 and 8 (as for PERCENTILE_EXC). If omitted, m defaults to 6. Thus QUARTILE_EXC(R1, k) = QUARTILE.EXC(R1, k) for k = 1, 2 or 3, but QUARTILE_EXC(R1, 0) = MIN(R1) and QUARTILE_EXC(R1,4) = MAX(R1) instead of outputting an error value.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Hyndman, R. J., Fan, Y. (1996) Sample quantiles in statistical packages
https://www.amherst.edu/media/view/129116/original/Sample+Quantiles.pdf
Calder, S. (2023) How to calculate percentile in Excel?
https://www.simonsezit.com/article/calculate-percentile-in-excel/
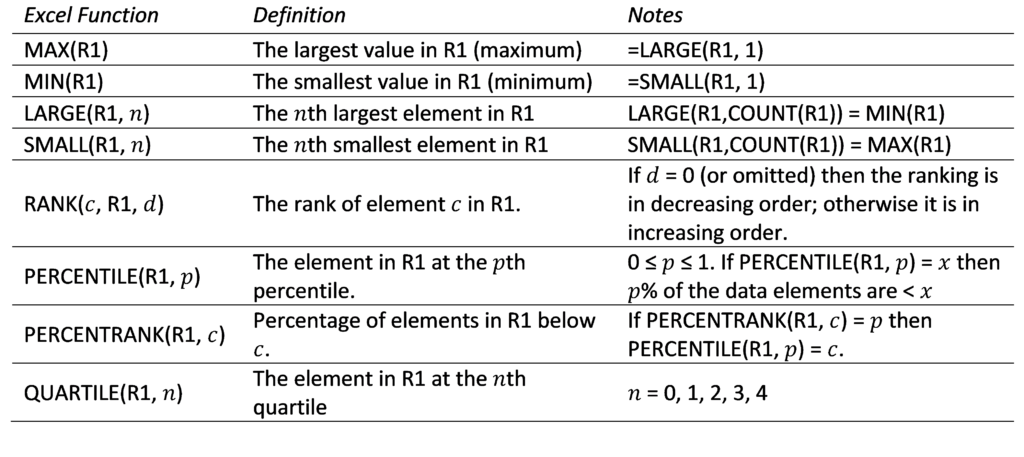
So I have a list of items that my company uses every day. The excel list is on an open file so that all 350 people can utilize it. I would like to find a way to rate the quality of each item, and then rank the list, automatically sorting it based on the top ranked item. The rating will come from employees (individually) once they are finished utilizing the item. Anyone know how to create something like this?
Brian,
You just need to sort the rankings. This can be done in Excel using Data > Sort&Filter|Sort. It can also be done by using the Real Statistics QSORT function.
Charles
I have 2 questions! 1st let’s assume we have list= [-1, 0, 2, 2, 2, 4, 5, 7] now how PERCENTRANK.INC(list, 2) and PERCENTRANK.INC(list, 3) calculates and 2nd now let’s assume we have list list= [-1, 0, 2, 2, 4, 5, 7] (now we have 2 2s in the list), how PERCENTRANK.INC(list, 2) and PERCENTRANK.INC(list, 3) calculates?
Sipan,
See the following webpage:
https://www.excelforum.com/excel-general/360841-algorithm-for-computing-excel-percentrank.html
Charles
Great article, it was very helpful.
Thank you very much for this!
Hi
Is this also the logic of how the Excel conditional formatting using 2 color scheeme with midpoint being Percentile works?
Thanks
Roni,
Sorry, but I don’t know what sort of logic Excel uses in this case.
Charles
Hello, We have a conflicting outputs of SQL (additionally other online tools ) and Excel percent rank functions.
The score to get percent rank for is : 100
The array is
86.36,87.501,88.642,89.783,90.924,92.065,93.206,94.347,95.488,96.629,97.77,97.78,98.001,98.222,98.443,98.664,98.885,99.106,99.327,99.548,99.769,99.99,100
From Excel the answer is 100 but from other tools it is 97.826 (in similar range)
Please help to clarify this ambiguity.
Thanks & Regards,
Harshad
Hello,
(re-posting since array was not clearly visible)
We have conflicting outputs of SQL (additionally other online tools ) and Excel percent rank functions.
The score to get percent rank for is : 100
The array is
86.36,87.501,88.642,89.783,90.924,92.065,93.206,94.347
,95.488,96.629,97.77,97.78,98.001,98.222,98.443,98.664,98.885,99.106
,99.327,99.548,99.769,99.99,100
From Excel the answer is 100 but from other tools it is 97.826 (in similar range)
Please help to clarify this ambiguity.
Thanks & Regards,
Harshad
Harshad,
What Excel formula are you using?
Charles
What if you have a set of 10,000 responses — let’s say the answers are 0-100 and some people don’t answer, so there are blanks for some responses. I don’t want them included in determining the percentile, but when I do the calc, Excel is using the blanks as zero in the calculation, but not including them in the count for that column. Is there an easy way to pull the blank answers out of the calculation for the percentile calculation? (Specifically I’m looking for 25th, 50th, and 75th percentiles.)
I’ve pretty much figured out how I can do this in a long, convoluted way, but before I do that, I thought I’d see if there was an easier way considering I have so many of these to look at.
Thanks in advance.
Never mind – I had to prove it to myself by doing it the hard way that Excel isn’t including non-numerical or blanks as zeros. It really isn’t. 😉
Suppose we have a class of 35 who appeared in a test.
1. If we want to calculate percentile, should we use formula which is the number of students below divided by total number of students multiply by 100 or we simply take highest number as 100 and calculate the rest on relative basis. 2. What should be the minimum total number to calculate percentile. What I mean is that if the total number is less, can we still calculate percentile. Is there any cutoff value?
Salim,
1. Either approach can be used, although the result won’t be the same. The referenced webpage explains how to calculate percentile using Excel.
2. There is no minimum total number, although obviously with a very small sample the value won’t have much meaning.
Charles
Hi,
Thank you for this helpful page!
I usually use PERCENTRANK since I think it’s a great function. The problem with this formula and also the same problem with RANK, LARGE, SMALL, etc is that the ranking gets equally distributed.
Imagine I have range of elements consisting of {1,2,3,4,10,20} then by using PERCENTRANK I get {0%,20%,40%,60%,80%,100%}, but the problem is that I don’t see how “far” from the others each value is. I would have preferred getting something like {0%,5%,10%,15%,50%,100%} if you understand what I mean (note: these percentages are just examples).
Is there any formula to help me get such a ranking?
Thank you.
Erik,
Perhaps you are looking for the formula =(x-MIN(R1))/(MAX(R1)-MIN(R1))
Charles
I’m sorry if this question is answered above and I just didn’t recognize it…
I would like to use the PERCENTRANK function to tell me the percent of data elements EQUAL TO and below c (not just below c).
Chuck,
In some sense PERCENTRANK already gives the percentile of data elements equal to or less than c. E.g. if range R contains the values 2, 5, 7, 8, 9, then PERCENTRANK(R,9) = 1 and PERCENTRANK(R,8) = .75. The problem comes in when R contains repeated values. If R contains the values 2, 5, 7, 8, 8, then PERCENTRANK(R,8) = .75 and PERCENTRANK(R,7) = .50.
If you strictly want the percentage of values in R less than or equal to some value c, then you can use the formula =COUNTIF(R,”<="&c)/COUNT(R). Here you need to replace R by an actual range (e.g. A1:B5) and c by an actual number or reference to a number (e.g. 5 or C4 or C4/2). Note that I have just updated the referenced webpage with a clearer, but admittedly nor completely clear, version of the subject. Charles
Dear Chalers,
I have 100 of sample and want to analysis factors affecting to information sharing patter and used five factors and asked to rank them from 1-5. Most important one rank as 1 and least important one as 5.
can I use the above ranking function to list the most important to least important factor ? or do i need to calculate mean rank value for each factor and decide which factor is most important?
Dear Nirosha,
You can certainly use the ranking function to list the most important to least important fact, but I don’t have enough information to tell whether this is sufficient for your underlying needs.
Charles
Dear Charles,
Thank you very much.let me explain bit more. I want to analysis farmers information sharing pattern using perception of farmer. I used 100 farmers and mentioned 5 factors. then asked them to rank these factors as most important factor affecting to information sharing pattern as 5 and least important one as 1.
after my data collection, I have data with different value for each factor. then How I analysis/list most important to least important factor?
taking mean rank value for each factor ?
or is there any promising methods to analysis my data?
Dear Nirosha,
Thanks that is clearer for me. You can calculate the average rank for each factor, thereby ordering the factors in terms of their average rank. You don-t need to use the RANK or RANK.AVG function to do this when you only have 5 factors.
If you assume that the 100 farmers are representative of the population of farmers, then you can also do some statistical analysis to see whether the rankings that you obtained are representative of the population. E.g. factor A and B may have scores of 4.5 and 4.7 respectively, thereby showing that at least for your population of 100 farmers factor B is ranked as more important. This may or may not be representative of the entire population. You can test this for example using one/way ANOVA (along with some follow-up tests). This is described in the Real Statistics website.
Charles
thank you very much charles
Thanks for this, it is very helpful but there is one more piece I would like to see. If I have a dataset of numbers, for example a list of prices within a certain market, and I want to find out what percentile a given known number, price in this example, is within the sample is there an easy way I can calculate this without having to do a table showing all the percentiles and then matching my number to the nearest one?
Don’t the functions PERCENTILE, PERCENTILE.EXC and PERCENTILE.INC do what you want?
Charles
I have a simple problem with a formula for percent.
I have a ranking of U.S. states over a 3 yr period.
I have three unique lists, i.e. 2006 ranking of states, 2008 ranking of states and finally 2015 ranking of states.
Now, I’m attempting to get the percent increase or decrease of each state’s rank from year to year.
I’m using a simple percent formula (NEW – OLD)/OLD
so, say Alaska’s rank for 2006 was 10 then in 2008 it was 22 and in 2015 it’s 45.
I have a conditional format that expresses the formula answer as a percentage using delta triangles and color coding.
THe problem is that the percentage is treating the number normally (as if not in a ranking).
THe difference is that in my ranking if the STATE rank goes up (it actually goes down the list of rank) – opposite of what I need.
example: Alaska went from ranking #10 in 2006 to rank #22 in 2008. Excel sees this as ONLY A NUMBER THAT INCREASES. It is not seeing it as a number that went DOWN IN RANK.
Do you have any idea how to get EXCEL to adjust?
Bob,
The Excel RANK function has format RANK(x,R1,order). If order = 0 (or is omitted) then the ranking is in decreasing order. If order = 1 then the ranking is in ascending order. It sounds like you can get the desired result by changing the value of the order argument in the formula.
If this doesn’t do what you want then when you calculate a percentage p, use 1/p instead, which will change the order (unless p = 0).
Charles