Weighted Minkowski Distance

Weighted norm

The weighted norm for a vector X = (x₁, x₂, …, x_n) and weights W = (w₁, w₂, …, w_n), where each w_i ≥ 0 and w_i > 0 for at least one i, is defined by

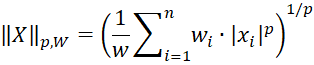where w = the sum of the w_i.

Weighted distance

The weighted Minkowski distance between vectors X and Y is ||X–Y||_p,W.

If y is a scalar, then  ||X–y||_p,W = ||X–Y||_p,W where Y is the vector all of whose elements are y.

For any p, 1 ≤ p ≤ 2, we can define

For p = 2, it turns out that L_p,W(X) is equal to the weighted mean. Similarly, for p = 1, L_p,W(X) is equal to the weighted median (see  Weighted Mean and Median).

See Lp Estimators for how to calculate the weighted Minkowski distance and weighted L_p,W(X) values in Excel.

References

Zornoza, J. (2020) Distance metric for machine learning. Aigents
https://aigents.co/data-science-blog/publication/distance-metrics-for-machine-learning

Wikipedia (2020) Minkowski distance
https://en.wikipedia.org/wiki/Minkowski_distance