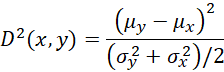Credit Scoring Divergence

Basic Concepts

(Credit Scoring) Divergence Statistic: Given two finite distributions p and q with corresponding elements x₁, …, x_n and y₁, …, y_n, we define the divergence measure as

This metric is used for credit scoring and is essentially the square of the effect size for the two-sample t-test where the two variances are weighted equally.

Example

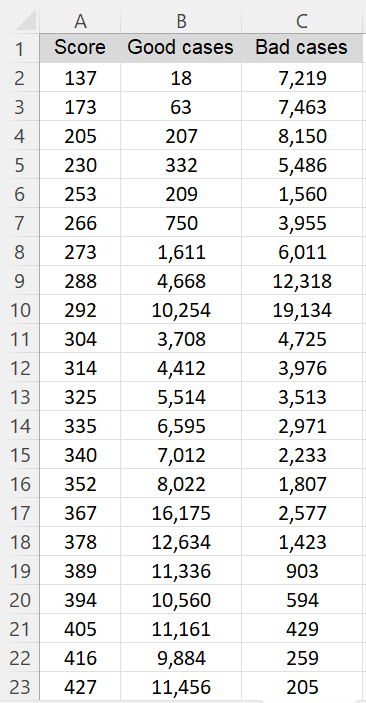
Example 1: Calculate the divergence statistic for the data in Figure 1. Here we view column A as containing data and columns B and C as containing the corresponding frequencies for the two samples.

Figure 1 – Credit scoring data

The calculation of the divergence is shown in Figure B. Column I shows the formulas used in column G.

Figure 2 – Divergence measure

Worksheet Function

Real Statistics Function: The Real Statistics Resource Pack provides the CS_DIVERGE worksheet function that calculates the divergence measurement for credit scoring. This function takes any of the following formats:

CS_DIVERGE(R1): an array R1 that contains three columns: the first column contains data values and the second and third columns contain frequencies (non-negative integers) for the two samples

CS_DIVERGE(R1): an array R1 that contains two columns consisting of the data for two samples

CS_DIVERGE(R1, R2): column arrays R1 and R2 that contain the data for two samples

CS_DIVERGE(R1, R2, R3): column arrays R1, R2, and R3: R1 contains data values and R2 and R3 contain frequencies for the two samples

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Open Risk (2022) Divergence statistic
https://www.openriskmanual.org/wiki/Divergence_Statistic

Zeng, G. (2013) Metric divergence measures and information value in credit scoring
https://www.hindawi.com/journals/jmath/2013/848271/