On this webpage, we provide proofs for the properties described in Basic Concepts of Correlation.
Property 4
Property 4: For constant a and random variables x, y, and z, the following are true both for the sample and population definitions of covariance
- cov(x, y) = cov(y, x)
- cov(x, x) = var(x)
- cov(a, y) = 0
- cov(ax, y) = a · cov(x, y)
- cov(x+z, y) = cov(x, y) + cov(z, y)
Proof: We give the proofs for the population version of covariance. The proofs for the sample versions are similar.
a) Clear from the definition of covariance
b) Clear from the definitions of covariance and variance
c) Follows from
d) Follows from
![]()
e) Follows from
![]()
Property A: If x and y are random variables and z = ax + b where a and b are constants then the correlation coefficient between x and y is the same as the correlation coefficient between z and y.
Proof: By Property 4
By Property 3 of Expectation
and so stdev(z) = a · stdev(x). Thus
![]()
Properties 1 and 2
Property 1
Proof: Let
![]()
Collecting identical terms, together with a change in summation indices, we find:
and so
from which the result follows.
Property 2:
Proof: The proof is similar to the proof of Property 1.
Other Properties
Property 3:
Proof: The proof is similar to that of Property 2 of Expectation.
Property 5: The following is true for both the sample and population definitions of covariance:
If x and y are independent then cov(x, y) = 0
Proof: The proof follows from Property 1d of Expectation and Property 3.
Property 6: The following are true both for samples and populations:
![]()
Proof: We give the proof of the first property for the population. The proof of the sample case is similar, as is the proof of the second property. By Property 2 of Expectation and Property 3
![]()
![]()
![]()
![]() References
References
Howell, D. C. (2010) Statistical methods for psychology, 7th Ed. Wadsworth. Cengage Learning
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf
Wikipedia (2012) Correlation coefficient
https://en.wikipedia.org/wiki/Correlation_coefficient
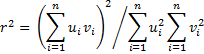
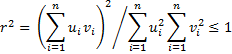
Dear Charles,
I believe there is an error in proof of Property A.d). After the second equality sign it should read:
E[((x-\mu_x) + (z-\mu_z))(y-\mu_y)]
otherwise the result will not follow.
Regards
Marc
Marc,
Thanks for catching this error. I have now corrected the formulas on the webpage.
I appreciate your help in improving the quality of the Real Statistics website.
Charles
I am confused by the term ” Average variance extracted (AVE)”. Dr. Charles, can you please explain this to me? Thank you.
Natalie,
I don’t see this term on the webpage that you are referencing. Are you referring to a term that I use on the website or is a term you found somewhere else? Generally this is a term used with Factor Analysis.
Charles