Basic Concepts
From Definition 3 and Property 1 of Method of Least Squares for Multiple Regression, recall that
If XTX is singular, i.e. doesn’t have an inverse (see Matrix Operations), then B won’t be defined, and as a result, Y-hat will not be defined. This occurs when one column in X is a non-trivial linear combination of some other columns in X, i.e. one independent variable is a non-trivial linear combination of the other independent variables. Even when XTX is almost singular, i.e. det(XTX) is close to zero, the values of B and Y-hat will be unstable; i.e. small changes in X may result in significant changes in B and Y-hat. Such a situation is called multicollinearity, or simply collinearity, and should be avoided.
Simple Example
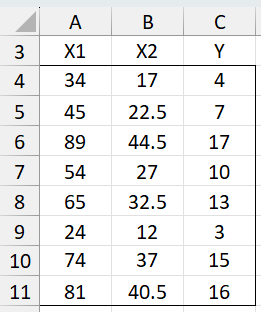
For example, in Figure 1, X1 is double X2. Thus XTX is singular. Excel detects this and creates a regression model equivalent to that obtained by simply eliminating column X2.
Figure 1 – Collinearity
Observations
In the case where k = 2, the coefficient estimates produced by the least square process turn out to be
If x1 and x2 are correlated, i.e.
then the denominators of the coefficients are zero and so the coefficients are undefined.
Unfortunately, you can’t always count on one column being an exact linear combination of the others. Even when one column is almost a linear combination of the other columns, an unstable situation can result. We now define some metrics that help determine whether such a situation is likely.
Definitions
Definition 1: Tolerance is 1 – , where
i.e. the multiple coefficient between xj and all the other independent variables. The variance inflation factor (VIF) is the reciprocal of the tolerance.
Tolerance ranges from 0 to 1. We want a low value of VIF and a high value of tolerance. A tolerance value of less than 0.1 is a red alert, while values below 0.2 can be cause for concern.
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource contains the following worksheet functions:
TOLERANCE(R1, j) = Tolerance of the jth variable for the data in range R1; i.e. 1 –
VIF(R1, j) = VIF of the jth variable for the data in range R1
Note that TOLERANCE(R1, j) = 1–RSquare(R1, j)
Example
Example 1: Check the Tolerance and VIF for the data displayed in Figure 1 of Multiple Correlation (i.e. the data for the first 12 states in Example 1 of Multiple Correlation).
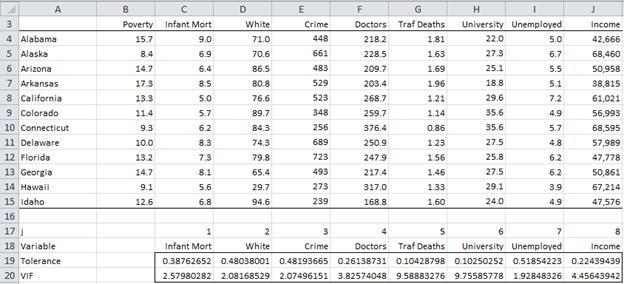
The top part of Figure 2 shows the data for the first 12 states in Example 1. From these data, we can calculate the Tolerance and VIF for each of the 8 independent variables.
Figure 2 – Tolerance and VIF
For example, to calculate the Tolerance for Crime we need to run the Regression data analysis tool inserting the range E4:E15 in the Input Y field of the dialog box (see Figure 2 of Real Statistics Support for Multiple Regression) and inserting the range C4:J15 excluding the E column in the Input X field. (To do this we first need to copy the data so that Input X consists of contiguous cells). We then see that Multiple R Square = .518, and so Tolerance = 1 – .518 = .482 and VIF = 1/.482 = 2.07.
Alternatively, we can use the Real Statistics formulas TOLERANCE(C4:J15,3) = .482 and VIF(C4:J15,3) = 2.07 (since Crime is the 3rd variable). The results are shown in rows 19 and 20 of Figure 2. Note that we should be concerned about the Traffic Deaths and University variables since their tolerance values are about .1.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Wikipedia (2012) Multicollinearity
https://en.wikipedia.org/wiki/Multicollinearity
Wasserman, L. (2010) Lecture notes for 36-707: linear regression
STATA (2023) Regression with STATA Chapter 2: regression diagnosis
https://stats.oarc.ucla.edu/stata/webbooks/reg/chapter2/stata-webbooksregressionwith-statachapter-2-regression-diagnostics/
Charles hi
apologies but somehow tolerance function is not working while VIF worked fine,
Separately, part_correl is not working either,
i am using xreal for Mac.
Any ideas?
Hello Yerzhan,
If you email me an Excel file with your data and results, I will try to figure out what is going wrong.
Charles
Hi Charles,
I have a dataset with 15 independent variables, and my dependent variable is customer lifetime value. Within the dataset there are a number of IVs with high correlation to each other. The IVs have different scales.
My objective is to understand which IVs are most important to customer lifetime value, relative to each other. My dataset is ~18K rows.
What steps with excel would you recommend for me to be able to 1. deal with standardising the variables to the same scale and 2. running an analysis which reveals meaningful differences in importance between my correlated IVs, and non correlated IVs?
Thanks,
Renee
Hi Renee,
1. You can standardize the scales by using the STANDARDIZE function on the data in each column (i.e. each variable). See also
https://www.real-statistics.com/multiple-regression/standardized-regression-coefficients/
I am not saying that you should do this, especially since it won’t change the correlations, but this is how you can do it.
2. Calculating multiple correlation is equivalent to running a multiple regression and finding the square root of the R-square value. Thus, you can use all the typical regression approaches. In particular, you can test what happens to the correlation value when you leave out one or more of the independent variables.This sort of test is described at
https://www.real-statistics.com/multiple-regression/testing-significance-extra-variables-regression-model/
Other webpages that might be helpful are:
https://www.real-statistics.com/multiple-regression/stepwise-regression/
https://www.real-statistics.com/multiple-regression/shapley-owen-decomposition/
Charles
Hello Charles,
I have a problem case with 16 independent variables (IV). I’ve checked the VIF’s and there are 4 IV’s with high VIF (>10 – this is the rule of thumb I am going by). I have a few questions:
1. I ran a regression on these 4 IVs (with high VIF) against the dependent variable and compared it with another regression with 3 IVs (with high VIF) removing one IV to see what happens. I’m not sure what I’m doing here but what I notice is that the VIF of one of the 3IVs significantly changed after I removed the 4th IV. What does this mean and how can I interpret it?
2. Since I have 4 IVs with high VIF, how can I identify which of the IVs have collinearity with each other? Because it could either be that the 4 IVs are all multicollinear or that 2 sets of the IVs are multicollinear.
3. How do I do a factor analysis to reduce the number of IVs? Do I group together these 4 IVs with high VIF or do I first identify which IVs are in fact causing multicollinearity against the other and do factor analysis on those?
Looking forward to your guidance!
Hello Maryam,
1. VIF is 1/Tolerance and Tolerance is 1-R^2 where R^2 is calculated for the linear regression that uses the independent variable under consideration as the DV and the other independent variables as IVs. Clearly, by leaving out one of the IVs the R^2 will change (and in fact should get lower). Suppose you have IVs x1, x2, x3, x4 and x1 and x4 are highly correlated, then it is not surprising that removing x4 might significantly change the VIF value for x1. I suggest that you trying doing this using some specific values. E.g. you can make the values of x4 equal x1+RAND(); provided the values of x1 are relatively large compared to 1, the values of v4 will be correlated to those in v1 (but not exactly 1)
2. This is a good question. I suggest that you try the following experiment where range A1:D10 contains the independent variable values for x1, x2, x3 and x4 and range E1:E10 contains the values for the dependent variable.
Case 1: Create near collinearity between x1, x2, x3 and x4. This can be done by placing the formula =RANDBETWEEN(1,40) in range B1:E10. Then place the formula =SUM(B1:D1)+RAND() in cell A1, highlight range A1:A10 and press Ctrl-D. Now run the regression and see what the VIF values are. They should all be high. Now rerun the regression leaving out any of the independent variables (leaving out x1, i.e. column A should be the easiest). You should expect that the VIF should be reduced.
Case 2: Create near collinearity between x1 and x3 and between x2 and x4. This can be done by placing the formula =RANDBETWEEN(1,40) in range C1:E10. Then place the formula =C1+RAND() in cell A1, highlight range A1:B10 and press Ctrl-R and Ctrl-D. Now run the regression and see what the VIF values are. They should all be high. Now rerun the regression leaving out any of the independent variables. This time you should expect that the VIF should remain high. In fact, you need to leave out two variables to reduce the VIF (but not x1 and x2 or x3 and x4).
You might need to tweak this a bit since I haven’t really thought out the situation completely. I hope you get the idea though.
3. I have not thought this out either, but you can run an experiment like the one I suggested above.
Charles
good day sir,
I wanna ask you for something.. how can I getting rid of multicollenearity.. iam doing a model with GDP equation (GDP= Consumption+Investment+Government expindeture+ x-im) and VIF is very high, how can i getting rid of it in excel by using The first difference.
Thanks alot.
One approach is to use Ridge Regression. See Ridge RegressionRidge Regression
Charles
Charles,
Would performing PCA on a set of variables allow us to avoid multicollinearity? I mean, the variability/variance effects could not be then linearly related, since, by orthogonality, they are pairwise – and overall – linearly independent?
Thanks in Advance.
Guero,
It sounds reasonable to me, although it is not clear why you would want to do this.
Charles
Sorry Charles,
I meant Factor Analysis, not PCA. I mean if there was collinearity of at least v1, v2, then we could blend one of them into a single factor?
Guero,
I think you are referencing your comment from one year ago.
In general if you have collinearity you could blend them into a single factor.
Charles
Charles,
What can I conclude if my correlation matrix has a lot of values close to 1, can I conclude (almost) collinearity from a high degree of correlation?
Also, say I have a model Y=a1x1+a2x2+…akxk
And I compute Y|Xi , i.e., I regress Y with respect to any of the Xi’s and I get
a coefficient ai close to 1 (and a high R^2) , can I conclude Xi is not needed in
the model? If Y|Xi = c+Xi then Xi is just a translate of Y and so provides no new
information?
Thanks.
You only need one value in the correlation matrix off the main diagonal to be close to 1 to have collinearity. It the two independent variables with a correlation of 1 are v1 and v2, then this would mean that v1 could be expressed as v1 = b * v2 + a for some constants a and b.
Note that you could have collinearity even when none of the elements in the correlation matrix are near 1. This could happen if you have three independent variables v1, v2 and v3 where v3 = v1 + v2.
Regarding your second question, I guess it depends on how you look at things. In some sense Xi is a great predictor of Y and so the other variables may not be needed (or at least they need to cancel each other out in some way). If indeed Xi is Y, then there is no point in including it among the independent variables.
Charles
Thank you Charles, you were very helpful.
Hi Charles,
So unless Tolerance is low and VIF is high, then we should not worry about multicollinearity? Even if two variables have very similar VIF and tolerance values but not necessarily low (tolerance) and high(VIF)?
Matt,
That is correct.
Charles
Hi Charles,
I am wondering why VIF consistently produces exactly 1.0 as the first VIF value. I just used the RAND() function to generate a bunch of columns and then used =VIF($F$58:$H$68,1). The output was exactly 1.0. I then proceeded to calculate VIF according to VIFi = 1/(1-R2i). To get exactly 1.0 the R2 value would have to be exactly 0.
Can you shed some light on it?
Wytek,
It is a good question. I will try to investigate this further and get back to you.
Charles
Good day sir, Please i want to no how to calculate mean effect. in-short, i need the step by step of how to calculate mean effect. The equation i have is confusing me.
Thanks. Emmanuel.
Sorry, but you need to be clearer about what you want. Mean effect for what?
Charles
In layman’s terms can you explain the danger in multicollinearity when performing multiple linear regression for predictive modeling purposes. I understand the issues it brings with interpretation of the model (strange parameter coefficients and p-values) but with respect to making predictions, what else should I know?
Ryan,
Essentially it means that one of the independent variables is not really necessary to the model because its effect/impact on the model is already captured by some of the other variables. This variable is not contributing anything extra to the predictions and can be removed. The danger is mathematical since it makes the model unstable in the sense that a small change in the values of this variable can have a big impact on the model.
You can think of it almost like 1/(a-b). If a and b are almost equal then the value of 1/(a-b) is very large; if a = b then its value is undefined (or infinity).
If you have true multicollinearity, then the “problem” variable will automatically be deleted by Excel. The real problem occurs when you don’t have exact multicollinearity (similar to the case where a = b), but close to multicollinearity (similar to the case where a is close to b). In this case, depending on the sophistication of the regression model, the “problem” variable won’t be eliminated, and the unstable situation described above can result.
Charles
Great explanation – very clear, thank you!
Charles,
Would it be helpful to do Gaussian elimination on X^TX in order to determine collinearity ? Or maybe we can somehow use the size of Det(X^TX) ; if it is close to 0 we suspect collinearity? I suspect there is a connection between PCA and collinearity; after PCA, it seems any collinearity would disappear, since the axes are pairwise perpendicular and are therefore linearly independent?
Thanks.
Sir,
I tried entering VER() and that give me 3.6.2 in the cell. (That should be the version number). But still VIF is not been calculated.
My Data in present in range A1:K23 with Header Row(Row 1) and Header Column(Col A), and formula i am using is =VIF(B2:K23,2)
Can i attach a file to this message? I am into the final Thesis of MBA program and this add-in could be a real help for me. Thank you.
Sir,
I am trying to use your add-in for Excel 2007 to calculate the VIF for my data but is giving me error:
” Compiler error in hidden module ”
and results in value error. Please guide what i am doing wrong.
Thank you.
Faseeh
Faseeh,
Try entering the formula =VER() in any blank cell in a worksheet. If you get an error, then the add-in was not installed properly. If you get the release number (e.g. 3.6.2) of the Real Statistics add-in then the cause is different and we will need to diagnose the problem in a different way.
Charles