When the conditions for Pearson’s chi-square test are not met, especially when one of more of the cells have expi < 5, an alternative approach with 2 × 2 contingency tables is to use Fisher’s exact test. Since this method is more computationally intense, it is best used for smaller samples.
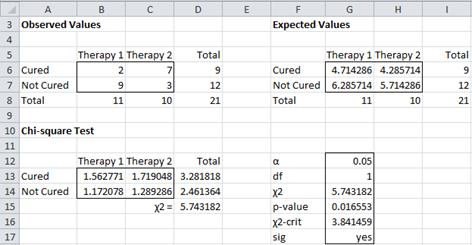
Example 1: Repeat Example 2 from Independence Testing using the data in range A5:D8 of Figure 1; i.e. determine whether the cure rate is independent of the therapy used.
Figure 1 – Data and Chi-square test for Example 1
As you can see from Figure 1, the expectation for two of the cells is less than 5. Since we are dealing with a 2 × 2 contingency table with relatively small sample size, it is better to use Fisher’s exact test.
The approach is to determine how many different ways the above marginal frequencies can be achieved and then determine the probability that the above observed cell configuration can be obtained merely by chance.
We can restrict our attention to any one of the cells since once the frequency for one cell is determined the frequencies for the other cells can be determined from the marginal totals. We choose cell B6 since it has the smallest marginal total (namely 9 in cell D6) and it is smaller than the other element that makes up this marginal total (namely 7 in cell C6).
Now cell B6 can take any value between 0 and 9; once this value is set the values of the other three cells can be adjusted to maintain the marginal totals.
The probability that cell B6 takes on a specific value x is equivalent to the probability of getting x successes in a sample of size 9 (cell D6) taken without replacement from a population of size 21 (cell D8) which contains 11 (cell B8) successful choices. This can be calculated by the hypergeometric distribution. Here cells D6 and B8 are cells with the marginal totals corresponding to cell B6 and cell D8 contains the grand total.
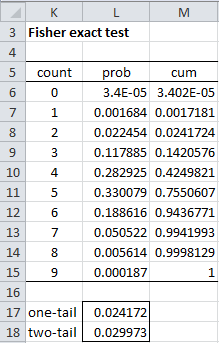
Figure 2 contains a table of the probabilities for each possible value of x.
Figure 2 – Fisher exact test for Example 1
Thus, e.g., cell L11 contains the formula
=HYPGEOMDIST(K11,$B$8,$D$6,$D$8)
Our test consists of determining whether the probability that at most 2 of those taking therapy 1 are cured (the observed count in cell B6) is less than .05. From Figure 2, we see that the probability of count 0 is 3.4E-05, the probability of count 1 is .001684 and the probability of count 2 is .022454 for a cumulative probability of .024172 < .05 = α, and so we reject the null hypothesis and conclude there is a significant difference between the cure rates for the two therapies.
There are one-tail and two-tail versions of the test. The p-value for the one tail test (cell L17) is given by the formula =SUM(L6:L8) or equivalently (for versions of Excel starting with Excel 2010)
= HYPGEOM.DIST(K8,B8,D6,D8,TRUE)
The p-value for the two tail test (cell L18) given by the formula
=SUM(L6:L8)+SUM(L14:L15)
where K14 is the leftmost cell in the right tail that has a pdf value ≤ L8 (since .005614 ≤ .022454, but .050522 > .022454). Equivalently, we can use the formula (for versons of Excel starting with Excel 2010)
= HYPGEOM.DIST(K8,B8,D6,D8,TRUE)+1−HYPGEOM.DIST(K13,B8,D6,D8,TRUE)
Real Statistics Excel Function: The following function is provided in the Real Statistics Resource Pack:
FISHERTEST(R1, tails) = the probability calculated by the Fisher Exact Test for a 2 × 2, 2 × 3, 2 × 4, 2 × 5, 2 × 6, 3 × 3 or 3 × 4 contingency table contained in range R1.
The range R1 must contain only numeric values. For a 2 × 2 contingency table, there is an optional second argument, tails = 1 (one-tailed test) or 2 (two tailed test, default). For other sized contingency tables only the p-value of the two-tailed test can be returned.
For Example 1, FISHERTEST(B6:C7,1) = .024172 and FISHERTEST(B6:C7, 2) = .029973.
Because the Fisher Exact tests can be resource intensive, limits have been placed on the sum of all the cells in the supported contingency tables. These limits are currently set at 2,000 for a 2 × 3 table, 1,200 for a 2 × 4 table, 440 for a 2 × 5 table , 200 for a 2 × 6 table, 280 for a 3 × 3 table and 100 for a 3 × 4 contingency table. Even close to these limits the processing can be quite slow. There are no limits for 2 × 2 tables.
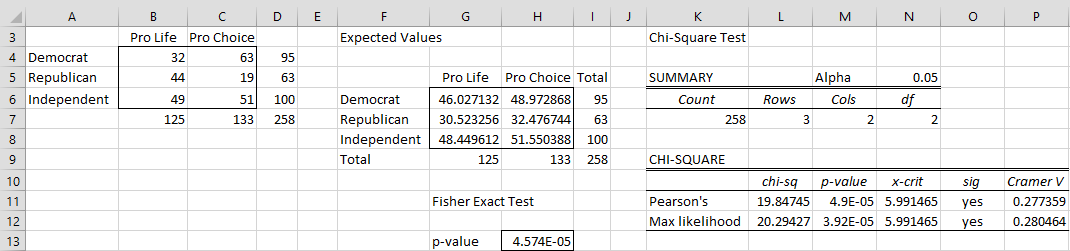
Example 2: Determine whether being pro-choice or pro-life is independent of a US citizen’s political party based on the sample shown in range A3:D7 of Figure 3.
We can use the Fisher Exact Test by using the formula =FISHERTEST(B4:C6). The result, as shown in cell H13 of Figure 3, is that being pro-choice or pro-life is not independent of party affiliation since p-value = 4.574E-06 < .05 = α (two-tailed test).
We can also use the Real Statistics Chi-square Test for Independence data analysis tool to get the same result (as shown on the right side of Figure 3), by checking the Fisher Exact Test option in the dialog box that appears (as shown in Figure 3 of Chi-square Test for Independence).
When I choose Chi-Squared test in RealStats, I don’t have an option to use Fisher’s exact test.
Brett,
What version of the Real Statistics software are you using? All the latest versions have a Fisher exact test option. You can find out the version number by entering the formula =VER()
Charles
Thanks Charles, I get the following:
4.4.3 Excel 2010/2013/2016
very informative
Hi Charles
I have data for 3 groups of people and 10 themes and I want to see if there is a significant difference between the 3 groups. I understand this is called a 10 x 3 matrix.
I would like to use the Fisher exact test.
Is there an excel ‘add in’ that I can use to do this?
If so could you post me the link, statistics are not my forte 🙂
Elle
Elle,
Why do you want to use Fisher Exact Test as opposed to Chi-square Test for some other test? In any case, I don’t know of an Excel version of a 3 x 10 Fisher test. The Real Statistics software can handle 3 x 3 tables.
Charles
Hi Charles
I have data for two groups ( exposed and non exposed to silica ) and I compare between the two groups by using fisher exact test but i can not detect p value for the variable (age). how can i do this?
age group 1 group 2
11-20: 0 2
21-30: 2 3
31-40: 1 2
41-50: 3 2
50-60: 2 1
> 60 : 1 0
This is a 6 x 2 contingency table. The Real Statistics software supports 5 x 2 tables but not 6 x 2 tables. If you combine the > 60 row with the row before it, you have a 5 x 2 table.
Charles
ok, thank you
but, what is the test?
11-20: 0 2
21-30: 2 3
31-40: 1 2
41-50: 3 2
> 50 : 3 1
The test is the one you asked for, namely the Fisher exact test, as described in the second part of the referenced webpage.
Charles
Hi Charles
Thank you for that.
I had intended to use the chi square but that is not possible as I have to many cells with 5 or under.
Hi Charles,
Can the Fisher test and hypergeometric distribution work with multiple binomial variables in a multidimensional (2^k) contingency table, or is it restricted to just two variables/dimensions? Is there an equivalent test and distribution for more than 2 binomial variables, especially where the frequency of some cells may be very low?
Kelvin,
If you are referring to m x n x d contingency tables, I guess that you could create a Fisher-like exact test, but I have not seen this done.
The Fisher exact test is so computationally intensive that even larger 3 x 3 or 2 x 4 tables are slow, I would expect that a 2 x 2 x 3 table would be very slow.
Charles
Thank you, Charles. So if Fisher’s test can’t work, I’m still struggling with this question of how to test for simultaneous correlation between multiple binomial variables?
Kelvin,
When you say binomial variables, do you mean (1) variables that have a binomial distribution or (2) dichotomous, i.e. only take one of 2 values?
Charles
2) dichotomous
Kelvin,
I can think of the following approaches for extending Fisher’s Exact Test to more than two dimensions
1. Use log-linear regression. This is described on the website for the three-dimensional case
2. Use logistic regression. This may be the easiest way of tackling the problem.
3. Write your own extension to Fisher’s exact test. You could probably do this for three dimensions,but the calculations would probably be quite slow.
Charles
Following your precious info and links, I realized a small implementation of the two-sided 2 x 3 test in excel.
I ‘d be delighted if you would accept it for testing.
Thank you for your amazing site.
Paolo
Paolo,
I would be delighted to accept it for testing. My email address can be found on the Contact Us link.
Many people have asked for 2 x 3, 3 x 3, etc. versions of the test and I haven’t had time to implement them yet. Your help would be appreciated by a lot of people, including me.
Charles
Hi Charles,
I downloaded your Resource Pack for Excel 2010. However when I used the FISHERTEST function on this 2×2 table:
3 11
7 1452
I get a P value of 1 when it should be 0.001.
Please advise
Thank you
Hoang
Hoang,
Yes, you are correct. The value calculated by the FISHERTEST function is not correct for this data. I will check to find out where the problem is.
Charles
Hi Hoang,
I have now fixed the bug in the FISHERTEST function. If you download the latest version of the software, Release 4.4.3, the function should give the correct answer. Thanks again for your help.
Charles
Thank you!
Hi Charles,
I have data from an experiment where I determined the frequency of 4 different categories (phenotypes) in a control group and want to compare the distribution to treated groups. The phenotypes are categorical and mutually exclusive. Categories are different and cannot be pooled.
For example, the control group has the following frequencies for a total of 20 observations:
A= 0
B= 0.95
C= 0.05
D= 0
If I look at two treated groups, they would show something like this:
Group 1: n= 70
A= 0
B= 0.76
C= 0.24
D= 0
Group 2: n=90
A= 0.2
B= 0.26
C= 0
D= 0.54
I calculated Confidence intervals at 95%, but how do I assign a statistical significance to the differences that I see? How do I compare to control or between samples? If these were numeric data, I would have done an ANOVA a long time ago, but this is not the case.
I would appreciate any help you could provide!
Diego
Diego,
It really depends on what you mean by “how do I assign a statistical significance to the differences”. Perhaps you are looking for a chi-square test of independence. In this case your would data look like
Cat..Control..Treat 1…Treat 2
A……….0……..0……..18
B………19…….53……..23
C……….1…….17………0
D……….0……..0……..49
Unfortunately, you can’t use the chi-square test since many of the cells are less than 5.
Please explain more carefully what you are trying to test.
Charles
Hello, can you use this for a bigger contingency table? (e.g. 2×5)
Hello Noelle,
No. This test applies only to a 2 x 2 table. There are versions for tables as large as 2 x 5, but I haven’t implemented them yet. The following is a reference for how to implement such a test in Excel.
http://www.amstat.org/sections/SRMS/Proceedings/y2001/Proceed/00541.pdf
Charles
It works a treat, Charles. Thanks so much.
John
John,
I just learnt of another error in the FISHERTEST function (a roundoff error). It probably very rarely occurs, but in any case I have corrected the problem, and so if you download the Release 4.02, which just went online a few minutes ago, you will have the corrected version.
Charles
Hi Charles,
Thanks for the prompt response. I downloaded from the section quoted below which is found on http://www.real-statistics.com/free-download/real-statistics-resource-pack/real-statistics-resource-pack-excel-2007/
“If you accept the License Agreement, click here on Real Statistics Resource Pack to download the latest version of the resource pack that accompanies this website (Release 3.8.1). This software is compatible with Excel 2007.”
Regards, John
John,
I don’t understand why you are having this problem. I am not seeing it on my computer. I plan to issue a new release of the software this week. I will make sure that this problem doesn’t occur with Excel 2007 (at least on my computer). Hopefully everything works fine on your computer with the next release of the Real Statistics software.
Charles
Many thanks for your efforts in looking, Charles. Let’s hope the new release works for me. If it doesn’t then it would be unfair of me to take yet more of your time.
John
John,
I expect to issue the new release tomorrow (Friday).
Charles
John,
Sorry, but today’s release does not fix the problem that you raised with the FISHERTEST function. The good news is that I have now identified the problem. What made it hard to find the problem was that the Excel HYPEGEOMETRIC function seems to give a different answer in Excel 2007 from that in Excel 2010/2013. I hope to put the fix in the software in the next few days. Note that the problem only arises in the two-tail test (not in the one-tail case).
Charles
Great news, Charles. Thanks again. Please let me know when you when you have fixed it.
John
John,
It should work in the latest version for Excel 2007, which I just put on the website.
Charles
Hi Charles,
I’ve downloaded Realstats for Excel 2007. A Fisher test on
1 12
17 53
gives an answer of 0.2800, which I trust is correct, and shows things are working.
But a test on
13 45
5 20
gives an error: #VALUE! with the explanation alongside: ” A value used in the formula is of the wrong data type”
If I change the 20 in this example, then a count of 13 or less gives a numeric answer but 14 or above gives a #VALUE error.
Cheers,
John (UK)
John,
I am not seeing this error message. I get a value of 1 in a two tail test and a value of .527 for a one-tail test. I fixed a bug in this function in Release 3.7. Are you using the latest release? If not this problem should be resolved if you upgrade to the latest release. If you are using the latest release, please let me know and I will investigate the problem further.
Charles
Dear Charles,
after installation I get with ctrl-m a list of statistic functions. But the FISHERTEST is missing.
What have I to do to add it to the list?
Thanks a lot. – Anyway your Add-in is great.
Christian
Christian,
FISHERTEST is a function and so you can use it just like any other Excel function (see example at the end of the referenced webpage).
Charles
Dear Charles,
I have downloaded the Real Statistics Resource Pack today – I have Excel 2011 for Mac. Like EMM, Rachel and Kristin, I do not seem to have FISHERTEST in the list of Realstats functions. When I directly type =FISHERTEST(B2:C3,1) or =FISHERTEST(B2:C3,2) for a 2×2 contingency table, I also get #VALUE! as a result. However, when I omit the tail and merely type in =FISHERTEST(B2:C3) I do get a result. Could you tell me how I can find out whether 1 or 2 tails have been used in the calculation? And how can I control the number of tails when I fail in the way described above?
Kind regards,
Maarten
Maarten,
If you leave out the second argument, it defaults to two-tails (which is the preferred test). I don’t know why inserting the second parameter results in an error in the Mac version of the software. I just checked and this is not the case for the Windows version of the software. Unfortunately, I don’t have access to a Mac computer at present so that I can resolve this problem. Once I get access to a Mac I will issue a new release which provides access to the 1-tailed test result.
Charles
Charles,
Many thanks for your quick reply. I am also able to run Windows separately on my Mac via VMWare Fusion. I have downloaded the Real Stats Resource Pack in Windows, and, as you mentioned, it does indeed work fine in there.
On another note, could you please tell me which method you used to compute the 2-tail P value? In my understanding there are three different methods to compute this?
Maarten
The function FISHERTEST does not seem to work for large values (I tried 4916/201/68/8)?
Gerald,
The problem is not with large values. In fact it even occurs for 3/2/2/3. The problem is that in the two-tailed test when the right and left critical regions overlap a p-value greater than 1 occurs since the overlapped area is counted twice. In these cases the correct p-value = 1. I will correct this in the next release, which I expect to deliver in the next day or two. Thanks again for finding the problem.
Charles
Thank you so much for your help and your brilliant add-in!
Sir
You should change ” .023172 < .05 = α" to "0.024172", and "FISHERTEST(B6:C7,1) = .023172" should be "0.024172".
BTW, I cannot understand the two-tailed test formula "=2*MIN(SUM(L6:L8),SUM(L8:L15),.5)."
Colin,
Thanks for catching another error. I have now corrected the typo. The two-tailed test is just twice the one-tailed test; the .5 entry is there just in case in order to make sure that the probability value is not larger than 1.
Charles
Sir
You wrote : “The probability that cell B6 takes on a specific value is equivalent to the probability of getting successes in a sample of size 9 (cell D6) taken with replacement from a population of size 21 (cell D8) which contains 11 (cell B8) successful choices. This can be calculated by the hypergeometric distribution. ”
According to above, should the Excel formula “=HYPGEOMDIST(K11,$B$8,$D$6,$D$8)” change to “=HYPGEOMDIST(K11,$D$6,$B$8,$D$8)”
Sir
I’ve checked the Excel Workbook you provided. The formula in this post is a typo.
Colin,
Use of your formulas will yield the same result.
Charles
Sir
It is very creative to use hypergometric distribution to solve this problem, you are very cool! But I think there is a typo in the following paragraph. Maybe you should change “with replacement” to “without replacement”. Is that right?
“ The probability that cell B6 takes on a specific value is equivalent to the probability of getting successes in a sample of size 9 (cell D6) taken with replacement from a population of size 21 (cell D8) which contains 11 (cell B8) successful choices. This can be calculated by the hypergeometric distribution. ”
Colin,
Another good catch. I have made the change that you have suggested.
Charles
I downloaded the Real Statistics Resource Pack, but I an unable to use perform a fisher test as advertised. It is not in the list of functions when I open Realstats, and it doesn’t work when I try entering the function directly into the cell either (=FISHERTEST(R1,t)). when I gry this I get #VALUE!. I am selecting only the 2×2 table for my data range and it is definitely only numeric data. Other functions work ( I tested the chi square function). FYI I have the 2007 version of excel.
Any suggestions?
Thank you.
I’m having this problem too – for some reason it will only allow me to perform the one-tailed Fisher’s Exact Test. I would really like to use the two-tailed test, if someone can shed some light on this…
Rachel,
I just retested the Real Statistics function =FISHERTEST(R1, tails) and it works properly for tails = 1 or 2. There was a problem several months ago, but it was resolved several releases ago. If you are not using a recent release I suggest that you download the latest release of the software.
Charles
I just downloaded the latest version of the software and am using it on some data in Excel. Interestingly, it worked on the first 2 x 2 table I used it on. However, on the next 2×2 table I tried it on, it gives me the #VALUE! error message. I wonder if it’s something to do with the numbers?
My first 2 x 2 table had the following numbers (from left to right top row, then bottom row): 82, 248, 75, 28
My second 2 x 2 table had the following numbers: 12, 179, 145, 97.
Any thoughts? I’m doing a two-tailed analysis. Thanks!
Kristin,
It worked on my computer. I got 3.16E-18 for the first problem and 2.76262E-34 for the second problem.
Charles