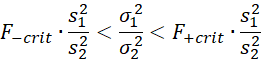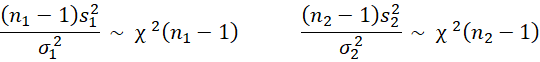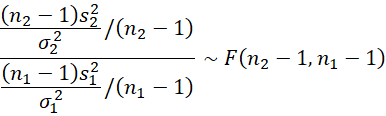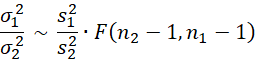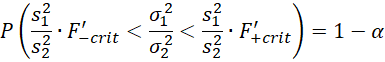Confidence Interval for Ratio of Variances

Basic Concepts

Property 1: If we draw two independent samples of size n₁ and n₂ with sample variances s₁² and s₂² from two normal populations with corresponding population variances σ₁² and σ₂², then

where F_+crit is the right critical value of F(n₂–1, n₁–1) and  F_–crit is the left critical value; i.e. F_+crit = F.INV.RT(α/2, n₂–1, n₁–1) and F_–crit = F.INV(α/2, n₂–1, n₁–1).

Proof: By Property 7 of Chi-square Distribution

By Definition 1 of F Distribution

from which it follows that

or equivalently

which means that

where F′_+crit is the right critical value of F(n₁–1, n₂–1) and  F′_–crit is the left critical value. This completes the proof.

Conclusion

Since, F.INV(α, df₁, df₂) = 1/F.INV.RT(α, df₂, df₁), we can express the confidence interval by

We can now use this property to calculate the confidence interval for the ratio of variances.

Example

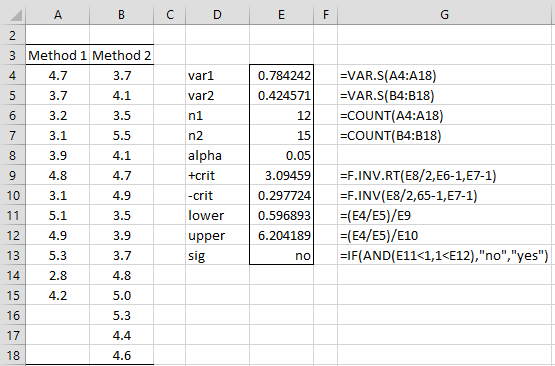
Example 1: Calculate a 95% confidence interval for the ratio of (population) variances based on the data from Example 1 of Two Sample Hypothesis Testing of the Variance.

The calculation of the confidence interval is shown in Figure 1.

Figure 1 – Confidence interval for variance ratio

A ratio of 1 means that the two population variances are equal. Since 1 is in the confidence interval (.597, 6.204), once again we have a non-significant result; i.e. we cannot conclude that the two population variances are different.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Links

↑ Chi-square and F distributions

References

PennState (2023) Confidence intervals for variances. Introduction to Mathematical Statistics
https://online.stat.psu.edu/stat415/book/export/html/810

Srivatsan, R. (2020) Confidence interval for the ratio of population variances. CountBio
http://www.countbio.com/web_pages/left_object/R_for_biology/R_biostatistics_part-1/confidence_interval_variance_ratio.html

Watts, V. (2022) Statistical inference for two population variances
https://ecampusontario.pressbooks.pub/introstats/chapter/11-3-statistical-inference-for-two-population-variances/