The Cochran-Mantel-Haenszel (CMH) test is used to test multiple 2 ⨯ 2 contingency tables across different values of a confounding variable. The test determines whether there is a significant difference between the odds ratios across the different values of the confounding variable.
We represent each of the k 2 ⨯ 2 contingency as shown in Figure 1.
Odds Ratio
The odds ratio (see Effect Size for Chi-square Tests) for contingency table i is then
For example, if Factor B represents Has a Heart Attack (Yes in column 1 and No in column 2) and Factor A represents Statin Taken (Yes in row 1 and No/placebo in row 2), then the odds ratio measures whether taking statins has an impact on the rate of heart attacks.
An odds ratio greater than one indicates that the drug has a positive effect in reducing the rate of heart attacks, while a value less than one indicates that the drug has a negative effect by not decreasing or even increasing heart attacks. Actually, the phrasing just used is misleading since it suggests a cause and effect. Instead, we are just measuring the association between the use of statins and the rate of heart attacks. Finally, an odds ratio of one shows that there is no association between statins and the rate of heart attacks.
Hypothesis Testing
The CMH test is used to test the null hypothesis that
ORi = 1 for all i = 1, 2, …, k
We now define the common odds ratio r by
This is the odds ratio of factor A to factor B after removing the influence of the confounding factor (which has k values).
The null and alternative hypotheses for the CMH test can be viewed as H0: r = 1 and H1: r ≠ 1. Now let
The test statistic for the CMH test is
The test can be run with or without the Yates 0.5 continuity correction, although the correction generally gives slightly better results.
A significant result means that there is an association between the two factors represented in the contingency tables.
Confidence Interval
We can also use the following formulas to estimate a 1 – α confidence interval for r.
The confidence interval is then defined as follows:
where zcrit = NORM.S.INV(1–α/2).
Woolf’s Heterogeneity Test
There is also a Woolf’s Heterogeneity Test which tests the null hypothesis
OR1 = OR2 = …= ORk
Here the test statistic is
where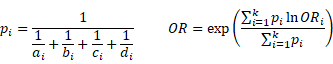 References
References
PennState (2017) Cochran-Mantel-Haenszel test
https://online.stat.psu.edu/stat504/lesson/5/5.3/5.3.5
SAS Help Center (2019) Cochran-Mantel-Haenszel statistics
https://documentation.sas.com/doc/en/pgmsascdc/9.4_3.4/statug/statug_freq_details92.htm
Moral de la Rubia, J., Valle de la O, A. (2023) Everything you wanted to know but could never find from the Cochran-Mantel-Haenszel test
https://www.scirp.org/pdf/jdaip_2023082810224634.pdf

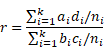
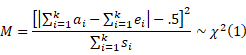
May I know if the odds ratios of Cochran Mantel Haenzel Effect Size and 95% C.I. is based on logistic regression?
I don’t know whether any of these metrics are based on Logistic regression.
I have just added some references to this web page. I believe that the second and third references provide this sort of information.
Charles