We now give some additional technical details about the chi-square distribution and provide proofs for some of the key propositions. Most of the proofs require some knowledge of calculus.
Chi-square Distribution
For any positive real number k, per Definition 1 of Chi-square Distribution, the chi-square distribution with k degrees of freedom, abbreviated χ2(k), has the probability density function
Using the notation of Gamma Function Advanced, the cumulative distribution function for x ≥ 0 is
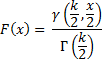
Properties and Proofs
Property A: The moment-generating function for a random variable with a χ2(k)distribution is
Proof:
Set y = x/2 (2θ–1). Then x = 2y/(1–2θ) and dx = 2 dy/(1–2θ). Thus
The result follows from the fact that by Definition 1 of Gamma Function
Property 1: The χ2(k) distribution has mean k and variance 2k
Proof: By Property A, the moment-generating function of χ2(k) is
and so
Since
it follows that
Thus
Property 2: Suppose x has standard normal distribution N(0,1) and let x1,…,xk be k independent sample values of x, then the random variable 
Proof: Since the xi are independent, so are the 
But since all the xi are samples from the same population, it follows that
Since x is a standard normal random variable, we have
Set y = x 
But since
is the pdf for N(0, 1), it follows that
Thus,
Combining the pieces, we have
But by Property A this is the moment generating function for χ2(k). Thus, by Theorem 1 of General Properties of Distributions, it follows that w has distribution χ2(k).
Property 4: If x and y are independent and x has distribution χ2(m) and y has distribution χ2(n), then x + y has distribution χ2(m + n)
Proof: Since x and y are independent, by Property A and Property 4 of General Properties of Distributions
But this is the moment-generating function for χ2(m + n), and so the result follows from the fact that a distribution is completely determined by its moment-generating function (Theorem 1 of General Properties of Distributions).
Property B: If x is normally distributed then x̄ and s2 are independent.
Proof: We won’t give the proof of this assertion here.
Property C: If z = x + y where x and y are independent and x has distribution χ2(m) and z has distribution χ2(n) with m < n, then y has distribution χ2(n–m).
Proof: Since x and y are independent, by Property 4 of General Properties of Distributions
and so by Property A
which means that
But this is the moment generating function for χ2(n–m), and so the result follows from Theorem 1 of General Properties of Distributions.
Property 5: If x is drawn from a normally distributed population N(μ,σ2) then for samples of size n the sample variance s2 has distribution
Proof: Since (x̄ – µ)2 is a constant and
we have
Dividing both sides by σ2 and rearranging terms we get
and so
Since x ~ N(μ, σ2) with each xi independently sampled from this distribution
By Property 2 it then follows that
Since the sampling distribution of the mean for data sampled from a normal distribution N(μ,σ2) is normal with mean μ and standard deviation σ/
and so by Property 2
By Property B, x̄ and s2 are independent and so the following random variables are also independent
and so by Property C
from which the proof follows.
Property 6: s2 is an unbiased, consistent estimator of the population variance
Proof (unbiased): From Property 5 and Property 1 it follows that:
Proof (consistent): From Property 1 and Property 3b of Expectation:
and so
References
Wikipedia (2013) Chi-square distribution
https://en.wikipedia.org/wiki/Chi-square_distribution
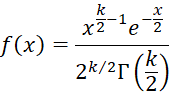
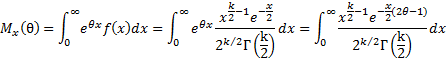
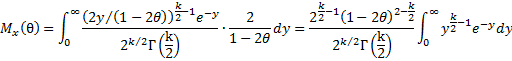
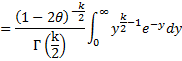
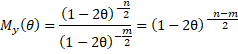
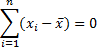
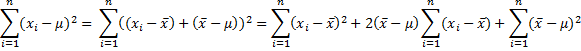
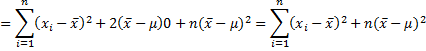
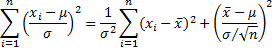
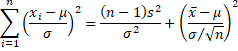
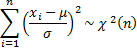
Hello Sir,
I am at a loss as to how to understand
(x_i-μ)/(σ) ~ N(μ,σ)
and
(x–μ)/(σ/sqrt(n)) ~ N(μ,σ) .
In my humble opinion, both of them would be distributed as N(0,1), based on what I’ve learnt in the Sampling Distributions. Could you please help me with this basic question?
Hello Jarl,
You are absolutely correct. I have just corrected these entries on the website. Thank you very much for identifying this error.
Charles
There is a mistake in your proof for the distribution of Theorem 2. It should only apply for large n.
You incorrectly apply moment generating functions when you say, “By Property 2, it follows that the remaining term in the equation is also chi-square with n – 1 degrees of freedom.” Property 2 only works for addition not subtraction, as $M_{X – Y}(\theta) = M_X(\theta) M_{-Y}(\theta) = M_X(\theta) M_Y(-\theta) = (1 – 2 \theta)^{-m/2} (1 + 2 \theta)^{-n/2}$ which is not exactly a chi-squared distribution.
This should be obvious when attempt to apply it to Z = X – Y where both X and Y are distributed chi-squared with 1 degree of freedom.
In retrospect, I am not sure if it is true or false, since the two terms are not independent.
Joseph,
Are you saying that you are not sure whether Theorem 2 is true or are you referring to something you said in your previous comment?
Charles
Hello Joseph,
Yes, there are mistakes in the proof, which I plan to correct shortly. I do believe that the theorem does not require large n since it uses the premise that x is normally distributed.
I appreciate your pointing out this error, thereby helping to improve the website.
Charles
Joseph,
I have just updated the proof. Hopefully, this time I have gotten it correct.
Charles
Excellent, helps me explain a lot of things!
Thanks for your analysis I take it for my assignment
I loved your explanation, I’ve been looking in many books for this.
Thank you for this easy to follow proofs.
This is refreshing and easy to follow for begginers. All too often many qualified/advanced staticians skip basic explanations and say ” …it is trivial to prove that… ” ; yet for the begginner, she/he would be expecting those very basics in order to come to a level where they will see the triviality! Thanks a lot and I will keep coming back for more as I am just starting statistics especially the mathematical statistics.
Sydeny,
Thanks for your comment. I try hard to give some of the theory and basic explanations, without getting too theoretical, for just the reasons you stated.
Charles