Central Limit Theorem: If x has a distribution with mean μ and standard deviation σ then for n sufficiently large, the variable
has a distribution that is approximately the standard normal distribution.
Proof: Using Properties 3 and 4 of General Properties of Distributions, and the fact that all the xi are independent with the same distribution, we have
Taking the natural log of both sides of the equation, we get
As we can see from the proof of Property 2 of General Properties of Distributions,
If we set z = all the terms on the right after 1 +, we have
Thus for sufficiently large n, |z| < 1. It then follows that
where q consists of all the terms in θk in the double expansion with k ≥ 3. Note too that the only function of n that each of these terms has in common is of the form n–k/2. Rearranging the terms, we have
Since and
, we conclude that
But as n → ∞ we see that nqθ3 → 0. Thus
By Property 3 of Normal Distribution, a random variable with standard normal distribution has the same moment generating function, and so the result follows from Corollary 1 of General Properties of Distributions.
References
Soch, J. (2020) Proof: Moment-generating function of the normal distribution. The book of statistical proofs
https://statproofbook.github.io/P/norm-mgf.html
Hoel, P. G. (1962) Introduction to mathematical statistics. Wiley
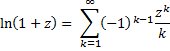
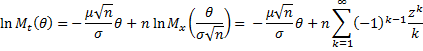
I like the concise nature of your mathematical calculation breakdowns in explaining the nature of the theorems and the statistical analysis tools you cover. Thank you for your information!
Jim,
Thank you for your comment. I do my best to make the information accessible.
Charles