In Statistical Power and Sample Size we show how to calculate the power and required sample size for a one-sample test using the normal distribution. On this webpage, we show how to do the same for a one-sample test using the binomial distribution. The process is similar, except that we need to take into account that the binomial distribution is a discrete distribution, unlike the normal distribution which is a continuous distribution.
In addition to the approaches described on this webpage, for large samples, by Corollary 1 of Relationship between Binomial and Normal Distributions, a random variable that has a binomial distribution can be approximated by a normal distribution, and so the techniques described in Statistical Power and Sample Size can also be used directly.
Power of a one-tailed test
Example 1: What is the power of the test in Example 3 of Hypothesis Testing for the Binomial Distribution?
For this example, we found 13 successes in a sample of size 24 and used a one-tailed test with α = .05 based on the binomial distribution with null and alternative hypotheses:
H0: p ≤ .35
H1: p > .35
As in Statistical Power of a Sample, to find the power of this test we must first calculate the critical value. This is done using the formula
xcrit = BINOM.INV(24, .35, 1−.05) = 12
This means that at least 95% of the distribution occurs for values x ≤ 12.
Figure 1 – Histogram of the distribution
In fact, 95.8% of the distribution is found to the left of the critical value (inclusive) since
BINOM.DIST(xcrit, n, p, TRUE) = BINOM.DIST(12, 24, .35, TRUE) = .9577
We calculate the power of the test using the following formula where pobs = 13/24 = .54167:
1 – BINOM.DIST(xcrit, n, pobs, TRUE) = 1 – BINOM.DIST(12, 24, .54167, TRUE) = 58.30%
We can chart the power of the test for various values of pobs as shown in Figure 2.
Figure 2 – Power Curve, one-tailed test
Here, cell N11 contains the formula =BINOM.DIST($O$8,$O$6,M11,TRUE) and cell O11 contains the formula =1−N11. We can fill in the rest of the table by highlighting the range N11:O22 and pressing Ctrl-D. We can create the line chart as described in Excel Charts.
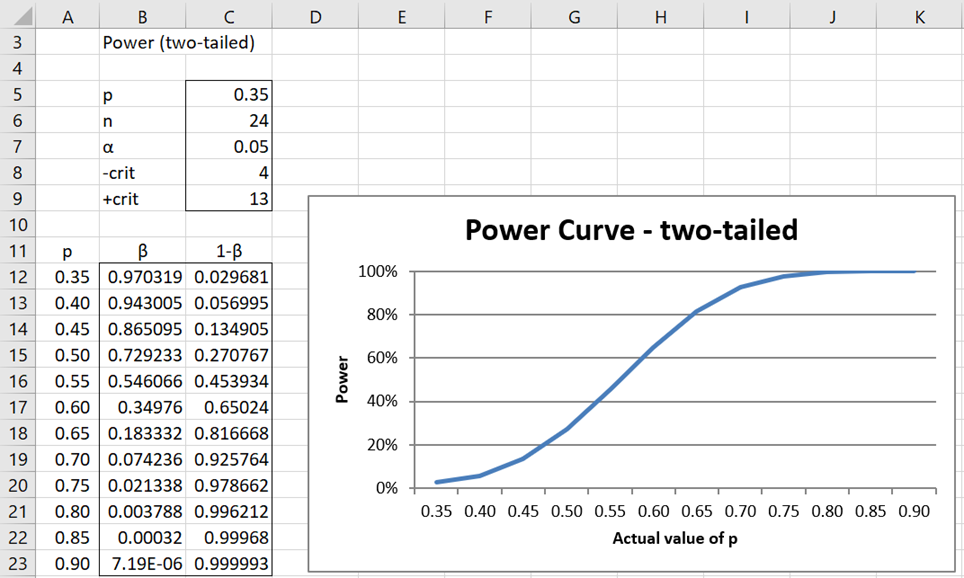
Power of a two-tailed test
Example 2: Repeat Example 1 for a two-tailed test.
This time there are two critical values: one on the right (x+crit) and one on the left (x-crit).
These are calculated as follows:
x+crit = BINOM.INV(24, .35, 1−.05/2) = 13
x-crit = BINOM.INV(24, .35, .05/2) = 4
The power of the test is calculated using the following formula where pobs = 13/24 = .54167:
= 1 + BINOM.DIST(x-crit−1, n, pobs, TRUE) – BINOM.DIST(x+crit, n, pobs, TRUE)
= 1 + BINOM.DIST(3, 24, .54167, TRUE) – BINOM.DIST(13, 24, .54167, TRUE) = 42.13%
We can chart the power of the test for various values of p as shown in Figure 3.
Figure 3 – Power Curve, two-tailed test
Real Statistics Function: The Real Statistics Resource Pack provides the following function to calculate the statistical power automatically.
BINOM_POWER(p0, p1, n, tails, α) = the power of a one-sample binomial test when p0 = probability of success on a single trial based on the null hypothesis, p1 = expected probability of success on a single trial, n = the sample size, tails = # of tails: 1 or 2 (default) and α = significance level (default .05).
Referring to Figure 2, we see that BINOM_POWER(.35, .45, 24, 1, .05) = .242. Referring to Figure 3, we see that BINOM_POWER(.35, .45, 24, 2, .05) = .134.
Real Statistics Data Analysis Tool
Real Statistics Data Analysis Tool: The Real Statistics Statistical Power and Sample Size data analysis tool can be used to determine the power of a one-sample binomial hypothesis test as well as the sample size required to achieve a specified statistical power target. See Statistical Power Data Analysis Tool for details.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Faul, F., Erdfelder, E., Buchner, A., Lang, A. G. (2009) Statistical power analyses using G*Power 3.1: Tests for correlation and regression analyses. Behavior Research Methods, 41, 1149-1160.
http://link.springer.com/article/10.3758/BRM.41.4.1149
Hanlon, B. and Larget, B. (2011) Power and sample size determination
http://pages.stat.wisc.edu/~st571-1/10-power-4.pdf


I have the following problem to resolve
Actual = 0
Population = 80
Probability = 1.5779%
How to find critical value for CL95% and CL99.9%
See https://real-statistics.com/binomial-and-related-distributions/proportion-distribution/
Charles
Hi Charles,
Firstly thank you for taking the time to respond to everyone’s questions and for maintaining the website! I have been relearning statistics for a task lately and the quality and usefulness of the information has been outstanding.
I’m currently having an issue with a problem I am trying to solve with the data below.
# of Tests: 50
# of Successes: 48
Minimum level of reliability for population: 95%
Is it possible to use this data to determine the probability that my total population’s reliability is at least 95%? Would the following formula below be correct? What about the case where all tests were successful, would it be possible to determine the probability that the reliability for the population is greater than 95%?
=BINOM.DIST(50,48,0.95,TRUE)
I have also done a similar calculation using a hypergeometric distribution when the population is smaller (<1000). Does the same principle still apply?
=HYPGEOM.DIST(#success, #trials, (reliability*population_size), population_size, TRUE)
Thanks in advance for all of your help.
Cheers,
Ian
Ian,
Thank you for your kind words. I am pleased that I am able to help people by answering questions and building up the website. It gives me great joy to learn new things myself and to share what I have learned with others. Sounds corny, but it is true.
I don’t know what you mean by “reliability”. The probability that at least 48 of the 50 tests will be successful is 1-BINOM.DIST(47,50,.95,TRUE) if the probability of succes on any single test is 95%, but I am not sure if this is what you are looking for.
Charles
Thank you for the comprehensive explanation.
Shouldn’t the power of the two-tailed test be:
1 + BINOMDIST(x-crit−1, n, pobs, TRUE) – BINOMDIST(x+crit, n, pobs, TRUE)
instead of:
1 − BINOMDIST(x-crit−1, n, pobs, TRUE) + BINOMDIST(x+crit, n, pobs, TRUE)
?
And I think the plot for the two-tailed test would look like one dip in the middle (at p=0.35) with the both side closer to 100% if it were extended to the left, correct?
I checked the results for the examples on the website with G*Power and I get the same answers based on the 1 − BINOMDIST(x-crit−1, n, pobs, TRUE) + BINOMDIST(x+crit, n, pobs, TRUE).
Charles
Charles,
I think it is worth to check the power equation for the example 2.
As ß should be out side of the critical region, it equals to
BINOMDIST(x+crit, n, pobs, TRUE) – BINOMDIST(x-crit-1, n, pobs, TRUE).
Therefore, power=1-ß=1-BINOMDIST(x+crit, n, pobs, TRUE) + BINOMDIST(x-crit-1, n, pobs, TRUE).
The equation in the current text render more than 1.
Sun Kim,
Why do you think that the value will be larger than 1? Can you give me an example where it is larger than 1?
Charles
Charles,
Using the example 2 information,
BINOMDIST(x+crit, n, probs, TRUE)
=BINOMDIST(14, 24, 0.542,TRUE)
=0.579
BINOMDIST(x-crit-1, n, probs, TRUE)
=BINOMDIST(3, 24, 0.542, TRUE)
=0.00003
If the currently written equation is used, then
1-BINOMDIST(x-crit-1, n, probs, TRUE) + BINOMDIST(x+crit, n, probs, TRUE)
=1 – 0.00003+0.579 >1.
I think there must have been mixed up with the right and left critical values in the current expression. As ß = BINOMDIST(x+crit, n, pobs, TRUE) – BINOMDIST(x-crit-1, n, pobs, TRUE),
1-ß can be expressed as the original inquirer stated.
I also double checked the values used in the power curve for the 2-sided test. The values listed in the current figures need to be redone. For instant, the first value listed in the power table, BINOM_POWER(0.35, 0.25, 24, 2,0.05)=0.029681 instead of 0.015968.
I do appreciate your effort presenting the accurate contents. I do really enjoy and appreciate the contents you provided in this website.
-Sun
Sun,
Thank you for pointing out the error in the formula. The calculations should be 1 + 0.00003 – 0.579 = .4215. I have now corrected the formula on the website.
The values in the power curve for the two-side test seem correct. E.g. the value in the table should be BINOM_POWER(.35,.35,24,2,.05), which .029681. The value of the second argument is .35 and not .25.
Charles
Thank you for your comment.
>I don’t see a post on November 4, 2018 for this webpage nor a Blog post. Where can I find this post?
The “Post” I mean the posts to this thread. This is one before my comment.
Anyway, in (2) of my last comment (“post”), you and I are in agreement.
For my (3), as you say, the result of the following calculation is .115541. That’s consistent with my last’ post’.
=1+BINOMDIST(3, 24, 0.25, TRUE)-BINOMDIST(13, 24, 0.25, TRUE)
But what I’m referring to is the 1-beta in Figure 3.
The value of the C12 cell of the Figure3 is 0.015968. My comments relate to this.
Why is the value of the C12 cell of the Figure3 0.015968?
Charles,
Anyway, “Why is the value of the C12 cell of the Figure3 0.015968?” is the most important part of my question.
————————
My previous comments may have confused you.
The “Post” I mean the following post.
https://www.real-statistics.com/binomial-and-related-distributions/statistical-power-binomial-distribution/comment-page-1/#comment-1275613
My comments (3) are detailed below;
Kim said, ”BINOM_POWER(0.35, 0.25, 24, 2,0.05)=0.029681 instead of 0.015968”. (see the Kim’s comment on October 17, 2018 at 3:31 am)
But Kim might have typo because the value of above Kim’s formula is 0.115541463 instead of 0.029681 and 0.015968.
Then you say that the second term of Kim’s equation should be 0.25 instead of 0.35 (see your November 4, 2018 at 7:30 pm ), but the result of the following formula is 0.029681407 instead of 0.015968.
= 1+BINOMDIST(3, 24, 0.35, TRUE)-BINOMDIST(13, 24, 0.35, TRUE)
Akihiro,
I now understand your comments. There was an error in the chart shown in Figure 3. I have now corrected it. Thank you for finding this error.
The formula in cell C12 is =1-B12 and the formula in cell B12 is =BINOMDIST($C$9,$C$6,A12,TRUE)-BINOMDIST($C$8-1,$C$6,A12,TRUE).
Cell C12 can also be calculated via the formula =BINOM_POWER(C5,A12,C6,C7).
I really appreciate your persistence in helping me locate the error. Thank you very much for improving the accuracy of the website.
Charles
Charles,
Thanks for the correction.
Whether I used your great macro or Binomdist, the calculated values of the betas in Fig3 matched.
Thank you !!
Dear Charles,
Thank you for this amazing post.
However, one thing I don’t quite understand is the P-obs. In the one-tailed test example, why is it 13/24?Since there are 14 successes in a sample size of 24, shouldn’t the Pobs be 14/24?
Thank you and have a great day!
Bobby,
Thanks for your question. 14 is a typing mistake. It should be 13.
I have now corrected the error.
Thanks for bringing this typo to my attention.
Charles
Dear Charles ,
First of all, I would like to thank you for this amazing web site, I have learned a lot of statistical technics in this amazing web site.
I have a question, i didn’t find in your website the theorical calclus of the formula of the power of one-tailed test based.
I can see that you have applied
1-beta =1 – BINOMDIST(xcrit, n, pobs, TRUE)
but how did you get it?
Thank you and have a great day!!
Khibox,
Glad you like the website.
The logic is explain at https://real-statistics.com/sampling-distributions/statistical-power-sample/
Charles