Required Sample Size for Binomial Testing

Goal Seek Approach

We now show how to determine the sample size required to achieve a specified power objective.

Example 1: A company has made a major improvement in its manufacturing process. They want to test whether this improvement will result in 80% of the components passing their quality assurance requirements instead of 35%. What sample size do they need to achieve 90% power based on a one-tailed test with a significance level of α = .01?

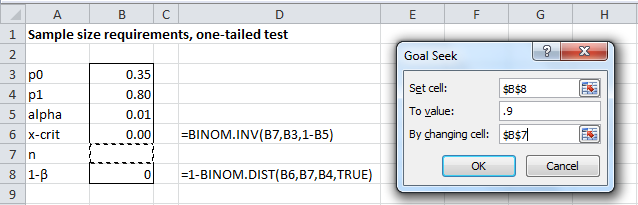
We capture the situation on the left side of Figure 1 (where n = 0 is an initial guess of the sample size) and use Excel’s Goal Seek capability, which is accessed as described in Goal Seeking and Solver.  We fill in the dialog box as shown on the right side of Figure 1 (see Statistical Power and Sample Size for further details).

Figure 1 – Goal Seek set-up to find required sample size

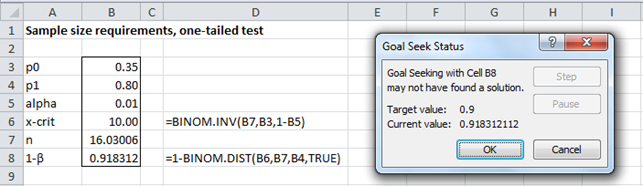
We now press the OK button on the dialog box. The results are shown in Figure 2.

Figure 2 – Goal Seek finds required sample size

Generally, we would round up the value in cell B7 to 17, but as you can see 16.03 is pretty close to 16. Thus, we should try putting 16 in cell B7 to see if the value in cell B8 is still at least .90. It turns out that it is. So a sample size of 16 is required.

Real Statistics Function

Caution: Goal Seek is not totally reliable for determining the sample size for the one-sample binomial test. In fact, if a different initial guess is made then the sample size calculated might be a little higher than the value generated above. The following Real Statistics function will give more reliable results.

Real Statistics Function: The Real Statistics Resource Pack provides the following function to calculate the sample size requirement automatically.

BINOM_SIZE(p0, p1, 1−β, tails, α) = the sample size of a one-sample binomial test required to achieve power of 1−β (default .8) when p0 = probability of success on a single trial based on the null hypothesis, p1 = expected probability of success on a single trial, tails = # of tails: 1 or 2 (default) and α = significance level (default .05).

The sample size required for a one-tailed test of Example 1 is BINOM_SIZE(.35, .80, .90, 1, .01) = 16. For a two-tailed test, the required sample size is BINOM_SIZE(.35, .80, .90, 2, .01) = 19.

Real Statistics Data Analysis Tool

Real Statistics Data Analysis Tool: The Real Statistics Statistical Power and Sample Size data analysis tool can be used to determine the sample size required to achieve a specified statistical power target. See Statistical Power Data Analysis Tool for details.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Excel Easy (2021) Goal Seek
https://www.excel-easy.com/examples/goal-seek.html

Faul, F., Erdfelder, E., Buchner, A., Lang, A. G. (2009) Statistical power analyses using G*Power 3.1: Tests for correlation and regression analyses. Behavior Research Methods, 41, 1149-1160.
http://link.springer.com/article/10.3758/BRM.41.4.1149

Hanlon, B. and Larget, B. (2011) Power and sample size determination
http://pages.stat.wisc.edu/~st571-1/10-power-4.pdf