Property A: The moment generating function for a random variable with distribution B(n, p) is
where q = 1 – p.
Proof: Using the definition of the binomial distribution and the definition of a moment generating function, we have
Observation: You can use the moment generating function to calculate the mean and variance (namely Property 1 of Binomial Distribution).
Property 1: If x is a random variable with distribution B(n, p), then for sufficiently large n, the distribution of the variable
where
Proof: By the linear transformation properties of the moment generating function (i.e Property 3 of General Properties of Distributions),
Taking the natural log of both sides, and then expanding the power series of 
Since p + q = 1 we have
If n is made sufficiently large 
Thus for sufficiently large n, |t| < 1. The ln term in the previous expression is ln(1+t) where |t|<1, and so we may expand this term as follows:
This means that
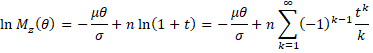
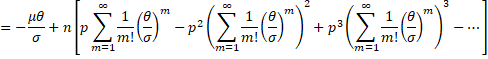
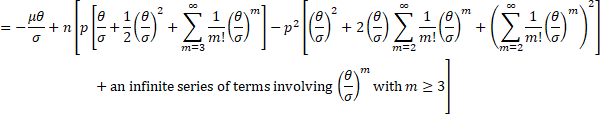By collecting terms in powers of θ/σ, we see that
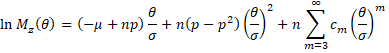
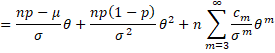
Here, the ck terms don’t involve n, σ or θ. Since μ = np and σ2 = np(1 – p), the coefficient of the θ term is 0 and the coefficient of the θ2 term is 1. Thus
Since the coefficient of each term in the sum has form
Thus
and so
But note that by Property 3 of Normal Distribution the moment generating function for a random variable z with distribution N(0, 1) is
The result now follows by Corollary 1 of General Properties of Distributions.
References
Hoel, P. (1962) Introduction to mathematical statistics, 3rd Ed. John Wiley and Sons
Bass, R. F. et al. (2020) Normal approximation to the binomial
Chapter 9 of Upper level undergraduate probability with actuarial and financial applications
https://probability.oer.math.uconn.edu/wp-content/uploads/sites/2187/2018/01/prob3160ch9.pdf
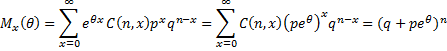
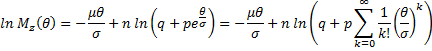
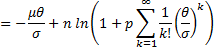
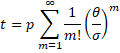
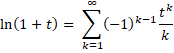
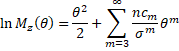
Good day Charles,
Is it possible there is a typo in the proof in the part just after :
“By collecting terms in powers of θ/σ, we see that :” ?
The exponent in the sum is (θ/σ)^3 where it seems to me it should be (θ/σ)^m.
Which would be more coherent with the rest.
Thank you,
Hello Yoan,
Yes, you are correct. The 3 should be an m. I have just corrected this on the webpage.
Thank you very much for finding this error and improving the accuracy of the website.
Charles
Is the z in ln(1+z) the same z as in z = (x-μ)/σ?
Hello Alan,
No, they should be different. Thank you for identifying this inconsistency in notation. I have now corrected this part of the proof.
I appreciate your help in making the website clearer and easier to understand.
Charles
At the part where you say “Here, the ck terms don’t involve n, σ or θ.” How does theta squared become divided by 2 and how does the sum change to include m in the exponents.
Hello,
I inadvertently left out the k! terms in the power series. In the second equation after the phrase “This means”, the p term should be divided by 1!, the p^2 term should be divided by 2! (this is the missing 2), the p^3 term should be divided by 3!, etc.
Since I previously used k as the index in two different sums, I had to change one of them to a different index: I chose m for this index. I see that this is confusing.
Thank you for your comment. I can see that I need to review the proof and correct the error and make things clearer.
Charles
At the part where you say “Rearranging the terms, we have”, how are you going from the expression containing an infinite series with z terms, to another expression containing an infinite series with c terms? I really don’t see it.
Attila,
I have redone the proof. I hope that this makes things clearer.
Charles
Thank you soooo much