Proportion Testing Analysis Tools

Worksheet Function

Real Statistics Function: The Real Statistics Resource Pack supplies the following function:

PropCI(p, n, lab, type, alpha): returns a column array with the lower and upper limits of the 1-alpha confidence interval for the proportion p based on a sample of size n; type = the type of the confidence interval with 0 = Wilson score (default), 1 = Agresti-Coull, 2 = Cooper-Pearson, 3 = Wald; default for alpha is .05; if lab = TRUE (default FALSE) an extra column of labels is appended to the output.

For example, if you place the array formula =PropCI(.3, 50, TRUE, 0, .05) in range A11:B12 of Figure 1 in Proportion Parameter Confidence Interval, the resulting values would be the same as those displayed in the figure.

Data Analysis Tool

Real Statistics Data Analysis Tool: The Real Statistics Resource Pack supplies the One-Sample Proportion Test and Two-Sample Proportion Test data analysis tools.

One-sample Example

Example 1: Use the One-Sample Proportion Test data analysis tool to determine whether the AIDS drug in Example 1 of Proportion Parameter Confidence Interval cures at least 50% of the patients. In this case, we want to test the null hypothesis π ≥ .5 (i.e. the population proportion is at least 50%) vs. the alternative hypothesis π < .5.

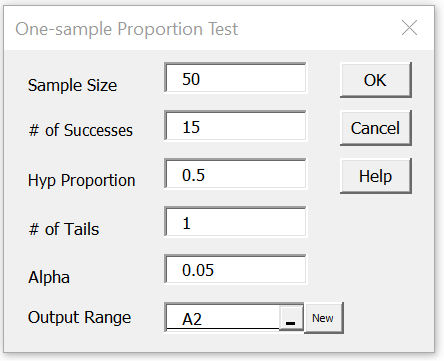
To accomplish this, press Ctrl-m and choose the One-Sample Proportion Test option from the Misc tab on the dialog that is displayed. Now, fill in the dialog box that is displayed as shown in Figure 1.

Figure 1 – One-sample Proportion Test dialog box

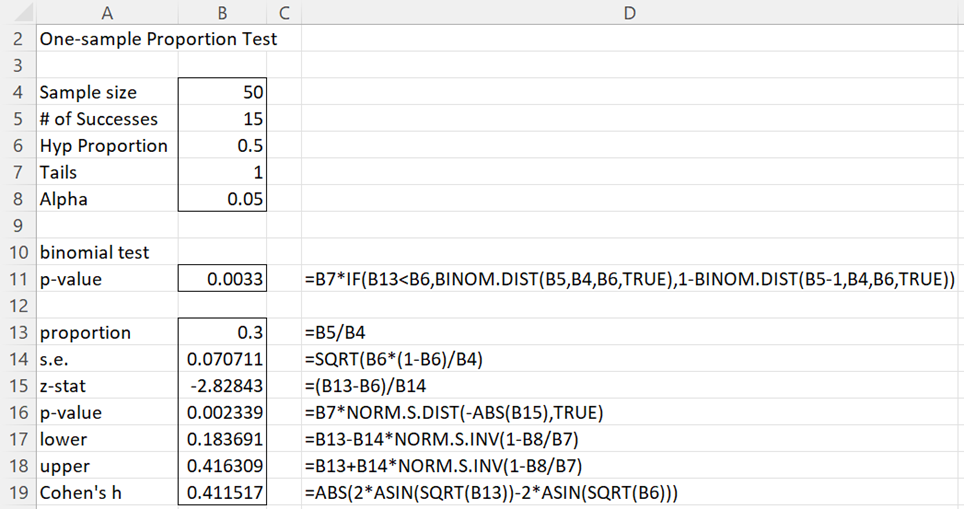
After clicking on the OK button, the output shown on the left side of Figure 2 is displayed. Column D displays the formulas used in column B.

Figure 2 – Output from One-sample Proportion Test

The p-value of either of the two tests is less than .05 (cells B11 and B16) and so we have a significant result. We conclude there is evidence to support the alternative hypothesis that less than 50% of the patients are cured.

Since this is a test of the left tail (observed proportion = .3 < .5 = hypothetical proportion), we also see (from cell B18) that the 95% confidence interval for the cure rate is (-∞, .416). Since this interval doesn’t contain .5, we again conclude that we have a significant result. Note that the value in cell B17 would have been used if the observed proportion were larger than the hypothetical proportion. In this case the confidence interval would have been (.184, ∞).

Finally note that Cohen’s h = .412, a little less than a medium effect.

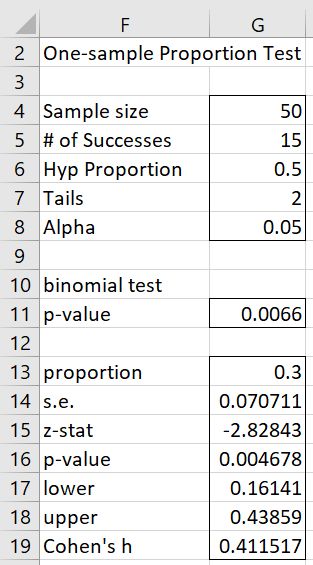
If we had run a two-tailed test (null hypothesis π = .5), then the results would be as shown in Figure 3. Note that we obtain the same results if we simply change the value in cell B7 from 1 to 2.

Figure 3 – Two-tailed test

This time the 95% confidence interval is (.161, .438). Note that this is the Wald interval. To obtain the other confidence intervals, you need to use the PropCI function as described above.

Two-sample Example

Example 2: Use the Two-Sample Proportion Test data analysis tool to obtain the results for Example 1 of Two-sample Proportion Testing.

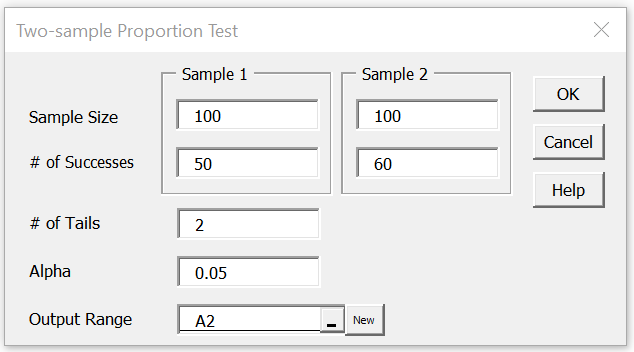
Press Ctrl-m and choose the Two-Sample Proportion Test option from the Misc tab on the dialog that is displayed. Now, fill in the dialog box that is displayed as shown in Figure 4.

Figure 4 – Two-sample Proportion Test dialog box

Upon clicking on the OK button, the results shown in Figure 5 appear (although the values in column D have been added so that you can see the formulas in column B).

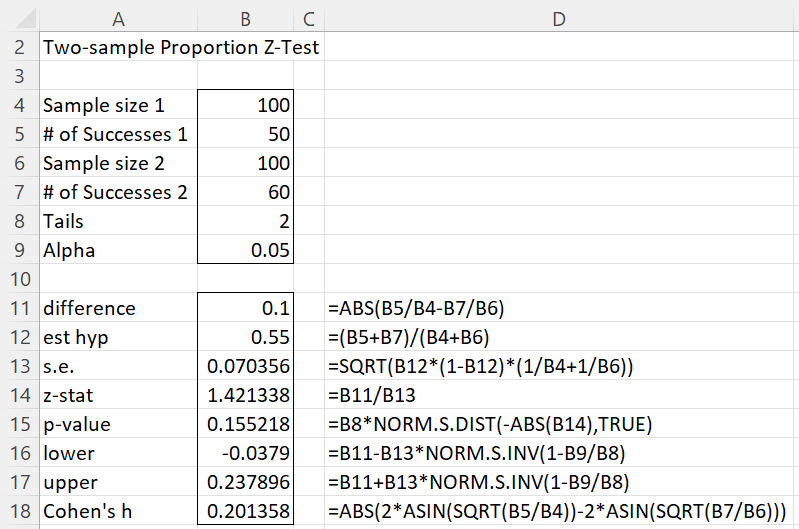
Figure 5 – Output from Two-sample Proportion Test

The results agree with those shown in Example 1 of Two-sample Proportion Testing. The 95% confidence interval is (-.0379, .238) and Cohen’s h effect size is .201, a small effect.

Caution: The Cohen’s h effect size reported by the Two-sample Proportion Test data analysis tool is incorrect. The formula in cell B18 of Figure 5 will contain SQRT(B7B6), resulting in a #NAME? error. You can manually insert the division symbol to get the correct answer. This bug will be fixed in Real Statistics Resource Pack Rel 8.8.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Influential Points (2020) Confidence intervals of proportions and rates
https://influentialpoints.com/Training/confidence_intervals_of_proportions-principles-properties-assumptions.htm

Wikipedia (2020) Binomial proportion confidence interval
https://en.wikipedia.org/wiki/Binomial_proportion_confidence_interval