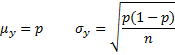Definition 1: If x is a random variable with binomial distribution B(n, p) then the random variable y = x/n is said to have the proportion distribution.
Properties
Property 1: If y has a proportion distribution then
Proof: By Property 1b of Expectation and Property 1a of Binomial Distribution
By Property 3b of Expectation
Property 1: Provided n is large enough – generally when np ≥ 5 and n (1 – p) ≥ 5 – then N(μy, σy2) is a good approximation for the proportion distribution for y with
Proof: This is a consequence of Property 1 of the Relationship between Binomial and Normal Distributions. This webpage also describes what “n large enough” means.
References
Saylor Academy (2012) The sample proportion. Introductory Statistics
https://saylordotorg.github.io/text_introductory-statistics/s10-03-the-sample-proportion.html
Wikipedia (2012) Population proportion
https://en.wikipedia.org/wiki/Population_proportion