Basic Concepts
Definition 1: The Poisson distribution has a probability distribution function (pdf) given by
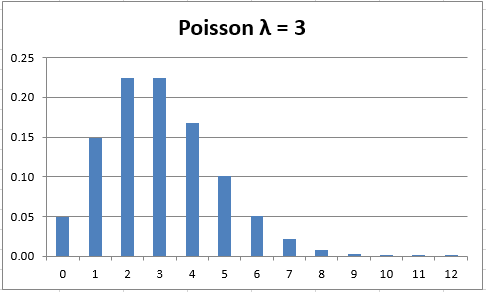
The parameter μ is often replaced by the symbol λ. A chart of the pdf of the Poisson distribution for λ = 3 is shown in Figure 1.
Figure 1 – Poisson Distribution
Observation: Some key statistical properties of the Poisson distribution are:
- Mean = µ
- Variance = µ
- Skewness = 1 /
- Kurtosis = 1/µ
Excel Function: Excel provides the following function for the Poisson distribution:
POISSON.DIST(x, μ, cum) = the probability density function value for the Poisson distribution with mean μ if cum = FALSE, and the corresponding cumulative probability distribution value if cum = TRUE.
Versions of Excel prior to 2010 do not support this function. Versions prior to Excel 2010 support the POISSON function, which is equivalent to POISSON.DIST.
Real Statistics Function: Excel doesn’t provide a worksheet function for the inverse of the Poisson distribution. Instead, you can use the following function provided by the Real Statistics Resource Pack.
POISSON_INV(p, μ) = smallest integer x such that POISSON(x, μ, TRUE) ≥ p
Poisson Process
If the average number of occurrences of a particular event in an hour (or some other unit of time) is μ and the arrival times are random without any tendency to bunch up (i.e. the assumptions for what is called a Poisson process) then the probability of x events occurring in an hour is given by
Example 1: A large department store sells on average 100 MP3 players a week. Assuming that purchases are as described in the above observation, what is the probability that the store will have to turn away potential buyers before the end if they stock 120 players? How many MP3 players should the store stock in order to make sure that it has a 99% probability of being able to supply a week’s demand?
The probability that they will sell ≤ 120 MP3 players in a week is
POISSON(120, 100, TRUE) = 0.977331
Thus, the answer to the first problem is 1 – 0.977331 = 0.022669, or about 2.3%. We can answer the second question by using successive approximations until we arrive at the correct answer. E.g. we could try x = 130, which is higher than 120. The cumulative Poisson is 0.998293, which is too high. We then pick x = 125 (halfway between 120 and 130). This yields 0.993202, which is a little too high, and so we try 123. This yields 0.988756, which a little too low, and so we finally arrive at 124, which has cumulative Poisson distribution of 0.991226.
Alternatively, you can arrive at the same answer (124) by using the Real Statistics formula =POISSON_INV(0.99,100).
Confidence Intervals
The 1–α confidence interval for the mean based on x events occurring (in a unit of time) is given by
For Excel 2007, χ2p,df = CHIINV(1−p,df).
See Chi-square Distribution for more details about the CHISQ.INV and CHIINV functions.
Example 2: Suppose the number of radioactive particles that hits a screen per second follows a Poisson process and suppose that 5 hits occurred in one second, find the 95% confidence interval for the mean number of hits per second.
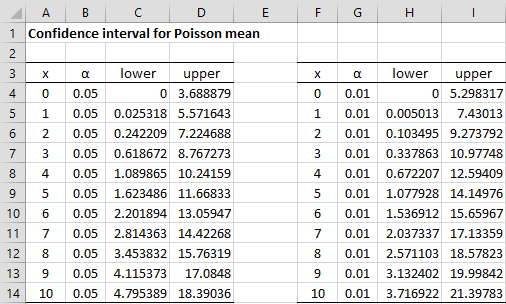
Figure 2 shows the confidence intervals for various values of x and α.
Figure 2 – Confidence intervals for the Poisson mean
The requested confidence interval is
1.623486 ≤ μ ≤ 11.66833
as calculated by the formulas in cells C9 and D9:
=CHISQ.INV(B9/2,2*A9)/2
=CHISQ.INV.RT(B9/2,2*(A9+1))/2
Note that CHISQ.INV(p,0) = #NUM! for any value of p, and so we cannot use this formula to calculate the lower bound when x = 0 (cell C4). In any case, this value is zero.
Relationship with Binomial and Normal Distributions
Property 1: If the probability p of success on a single trial approaches 0 while the number of trials n approaches infinity while the value of np stays fixed, then the binomial distribution B(n, p) approaches the Poisson distribution with mean μ = np.
Click here for the proof of this property.
Observation: Based on Property 1 the Poisson distribution can be used to estimate the binomial distribution when n ≥ 50 and p ≤ .01, preferably with np ≤ 5.
Example 3: A company produces high-precision bolts so that the probability of a defect is .05%. In a sample of 4,000 units, what is the probability of having more than 3 defects?
The probability is 14.3%. We obtain this probability by using the distribution B(4000, .0005), as follows:
1 – BINOMDIST(3, 4000, .0005, TRUE) = 1 – 0.857169 = 0.142831
We can also use the Poisson approximation as follows:
μ = np = 4000(.0005) = 2
1 – POISSON(3, 2, TRUE) = 1 – 0.857123 = 0.142877
As you can see the approximation is quite accurate.
Observation: The Poisson distribution can be approximated by the normal distribution, as shown in the following property.
Property 2: For n sufficiently large (usually n ≥ 20), if x has a Poisson distribution with mean μ, then x ~ N(μ, μ), i.e. a normal distribution with mean μ and variance μ.
Test for a Poisson Distribution
The index of dispersion of a data set or distribution is the variance divided by the mean.
Since the mean and variance of a Poisson distribution are equal, data that conform to a Poisson distribution must have an index of dispersion approximately equal to 1. We can use this fact to test whether a data set has a Poisson distribution, as described in Goodness of Fit.
In fact in Goodness of Fit, we also show how to use the chi-square goodness-of-fit test to determine whether a data set follows a Poisson distribution.
Difference between Two Poisson Distributions
If x and y are two independent Poisson distributed random variables, then x – y has a Skellam distribution as described at Skellam Distribution.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Wikipedia (2012) Poisson distribution
https://en.wikipedia.org/wiki/Poisson_distribution
NIST (2012) Poisson distribution
https://www.itl.nist.gov/div898/handbook/eda/section3/eda366j.htm
Given a set of datapoints, is it possible to approximate the values for a Poisson distribution equation in excel?
Hello Axel,
The Poisson distribution is specified by the lambda parameter. You can use the mean of the set of datapoints as an estimate for the lambda parameter. Also see
https://www.statlect.com/fundamentals-of-statistics/Poisson-distribution-maximum-likelihood
Charles
Given a graph, is it possible to approximate the lambda value of the poisson distribution?
Hello Axel,
The graph specifies the data points. You can then determine the lambda parameter as the mean of the data points (as described in my previous response).
Charles
for Poisson distributed samples, how do I compare two independent sample means for significance testing ?
For example: (50 events in 500 seconds vs. 39 events in 300 seconds).
How do i know if my duration is sufficient to count such rates ?
Is there any option for this in excel or R.
Hello Usha,
Are you testing the null hypothesis that the two samples come from the same Poisson distribution (i.e. they have the same mean)?
Charles
Yes.
How would you go about calculating win rates for multi variable poisson numbers like 3.5 vs 5.5, thank you
Evan
Hello Evan,
I don’t know what you mean by win rates. I also don’t know what you mean by multivariate poisson numbers.
Can you clarify your comment?
Charles
How would I find a certain number of occurrences or more? (in excel)
I know that to find for example 6 occurrences or less the function would be =POISSON.DIST (6,5.3,TRUE)
*where the mean is 5.3
Hello Brianna,
Prob(x>=6) = 1 – Prob(x<=5) Charles
Hi Charles
At the beginning of the article you mention kurtosis and Skew are key parameters of the Poisson Distribution. However, You never use Kurtosis or Skew anywhere in your excel example for calculating the cumulative probability distribution function.
Is there anywhere you input skew and kurtosis to get the accurate cumulative probability function for the data set?
Thank you
Hello Justin,
The population skewness and kurtosis statistics are completely determined by the mean, and so they are not needed when you calculate the cumulative probability function.
Charles
Thank you for the response Charles.
The number of hit can be addressed simultaneously on website is 35K and the average hit per min is 15K. the peak in last one year hit data is observed as 28K. Each hit is served in 5 sec on website. Need your assistance to calculate the number of maximum hit in next one year at any movement of time.
When you say “number of maximum hit in next one year at any movement of time”, do you mean the maximum number of hits in any year?
Charles
Hi Charles,
I am an English teacher and I’ve been trying to come up with a model to calculate the probability of students getting a determined score on a test based on a series of scores they previously obtained. I work with TOEFL and IELTS preparation courses, so we have students take the same test format over and over again.
Do you believe I would be able to use the poisson distribution to calculate that in Excel?
Thank you in advance! Cheers!
Hello Fabio,
Why do you believe that the data follows a Poisson distribution_
Charles
Hi Charles,
Thanks for your reply!
That’s a very good question. Actually, I have no idea. As a Language teacher, I am not very good at Maths, you know. However, I have been searching for a way to calculate the probability in that case and the Poisson Distribution seemed to be suitable. I saw an example on another blog where it was used to predict soccer game scores based on a set of results from previous matches, for example.
Although I know that when it comes to test taking things are quite complex and not so predictable, since the practice tests students take are pretty much alike, I would like to use this model to show them that just by retaking the same test – without studying more before that – their chances won’t improve much. Students often overestimate their chances, what sometimes makes them neglect their studies.
Anyway, long story short, maybe this model isn’t indeed suitable for that. For me, it was almost just like guessing that it would be. Thanks for your attention and help!
Hello Fabio,
Which of the following are you trying to study?
1. the student takes the same exact test many times without studying between?
2. the student takes the same test twice without studying between?
3. as for #1 except that it is not the same exact test but a standard test that is supposed to measure the same thing (such as the SAT)?
4. as for #2 except that it is not the same exact test but a standard test that is supposed to measure the same thing (such as the SAT)?
Charles
Hi Charles,
Alternatives 3 e 4 would best represent the scenarios I usually deal with (especially the 3rd one). The tests are not exactly the same in terms of content; however, the test structure and exercise types are very similar. I often work with TOEFL and IELTS exams.
Many thanks!
hi Charles,
In the finance community, an audit sampling method (monetary unit method) is using a confidence factor published by the American Institute of Certified Public Accountants. For example, for confidence level of 63% wherein the ratio of the expected misstatement to its tolerable misstatement is 50%, the confidence factor is 2.32. Similarly for a confidence level of 50%, the confidence factor is 1.37. How is this derived? The AICPA has disclosed that these statistical tables are based on poisson distribution.
Shirley
Hello Shirley,
I am sorry but I am not familiar with the AICPA guidelines and so I don’t know how they were derived.
Charles
Hi Charles,
Good Day!
I have calculated the Poisson inverse cumulative from my data using the formula
1-Poisson(x,u,True). Is this the same as the inverse cumulative frequency distribution of the data?
I have read some papers that the result is similar. But I have not found any way to solve or calculate the inverse cumulative frequency distribution of the data.
Thank you.
Hello,
The POISSON_INV function given on this webpage calculates the inverse cumulative frequency distribution of the data.
I don’t think that 1-Poisson(x,u,True) gives equivalent results.
Charles
I want to determine poisson distribution with kolmogorov smirnov with excell and R. How to calculate manual of poisson distribution in excell by using kolmogorov-smirnov? And if i use software R : ks.test(data,ecdf(data)). Is it true?
Ainul,
1. The following webpage shows how to use the KS test for the exponential distribution. The process is almost identical to the approach required for the Poisson distribution: https://real-statistics.com/non-parametric-tests/goodness-of-fit-tests/one-sample-kolmogorov-smirnov-test/
2. I don’t use R and so I am not familiar with ks.test(data,ecdf(data).
Charles
what about the data I have large size? for example : 1,16,30,102,130,133,40,4,38,119,221,259,310? if using excell and the result D > D table. what is the data is not poisson distribution?
Ainul,
If you are using the Kolmogorov-Smirnov test, then D > D-crit means that data does not come from a Poisson distribution. See
https://real-statistics.com/non-parametric-tests/goodness-of-fit-tests/one-sample-kolmogorov-smirnov-test/
Charles
A company publishes statistics concerning car quality. The initial quality score measures the number of problems per new car sold. For one year, Car A had 1.451.45 problems per car. Let the random variable X be equal to the number of problems with a newly purchased model A car. Complete (a) and (b) below.
A) If you purchased a model A car, what is the probability that the new car will have zero problems?
B) If you purchased a model A car, what is the probability that the new car more than 3 or fewer problems?
Hasten,
Assuming that the assumptions for the Poisson distribution are satisfied, these sorts of problems are described on the referenced webpage. Here your mean is 1451.45.
Charles
Hi Charles
Need help Poisson Distributiin.
Recently my team assignment selected Hotel beds unoccupied with 50 counts and our expected number=mean= lambda. However, my lambda = 34.36 that unable fit me to do the calculation.
My lecturer told to reduce lambda. My I know how to reduce the lambda for average of 34.36 for beds.
I found Lambda only able calculate not more than 10.
I hope to heard from you.
Thank you
Dickson,
Sorry, but without knowing more about your scenario I don’t know how to reduce lambda.
Charles
Hi Charles, by using excel to calculate the probability. Wat is =1-poisson.dist(X,Mean,True/False) VS =poisson.dist(,Mean,True/False)? When to use 1-Poisson?
Romanee,
If F(a) = the probably that x <= a, then 1 - F(a) = the probability that x > a.
Thus, =poisson.dist(X,Mean,True) is the probability that the Poisson distribution is less than or equal to X and
=1-poisson.dist(X,Mean,True) is the probability that the Poisson distribution is greater than X.
Note that this is not true if True is replaced by False.
Charles
Hi Charles,
If my question is
A sample of 32 hotels show that the mean of numbers of guests is 55, and I would like to find a P(100<=x<=150), is it correct my formula is =POISSON(150,55,TRUE)-POISSON(99,55,TRUE) ?
Hope you can assist me in this matter.
Thanks a lot.
Lena,
Assuming the data follows a Poisson distribution, then the formula you have given is correct.
Charles
Do I need to check whether the data is poisson distribution?
Or I need to testing the normal distribution using QQ plot…and etc?
Thanks Charles.
Lena,
1. If you know that the data should follow a Poisson distribution on theoretical grounds (e.g. there is a Poisson process), then you should be ok. One quick check to see whether data follows a Poisson process is to see whether the mean is roughly equal to the variance (as described on the website).
2. If you believe the data follows a Poisson distribution, then there is no reason to test for a normal distribution
Charles
1. Does it possible that the data set simultaneously follow a Poisson distribution and normal distribution?
2. If it follow a Poisson distribution, how to I find the P(X=O) ? When mean= 0.36667, SD=0.4901.
Hope you can assist me on this, thanks Charles.
Lena,
1. No
2. I am not sure what you mean by P(X=O), but you need to use the POISSON function.
Charles
As Poisson distribution is approximately normal, so can I use normal distribution as well in calculate the probability of discrete random variable?
Lena,
For n sufficiently large (usually n ≥ 20), if x has a Poisson distribution with mean μ, then x has an approximately normal distribution with mean μ and variance μ.
If n is sufficiently large, then, yes, you can use the normal distribution.
Charles
Dear Charles,
You state on this page that “The index of dispersion of a data set or distribution is the mean divided by the variance.” Isn’t the definition of the index of dispersion “the variance divided by the mean”?
Eugene.
Eugene,
Yes, you are correct. I have just changed the webpage to correct this error.
Thanks for your help in making the website more accurate.
Charles
Hi Charles,
Please help me with this problem as i do not understand how the standard deviation affects the processing time.
An analyst in the statistics office of a government department in Wellington
requests for reports. On average the office receives 19 requests per (40 hour) week, with the arrival pattern resembling a Poisson process. Once working on a request the processing time averages 2.0 hours with a standard deviation of 1.0 hours. After the request is processed the report is automatically emailed to the requester.
(a) What is the utilisation of the analyst?
(b) What is the average time a request waits before processing begins (Tq)?
Are my answers correct for (a) 0.2375 and (b) 0.6557?
Avi,
How did you calculate your answers?
Charles
I came across an article on the number of accidents per # man hours worked.
The article did not detail how the adjusted accident was derived. Neither did it specify how the UCL, Avg and LCL was derived based on the adjusted accident.
Need help to determine adjusted accident, UCL, Avg and LCL.
# man hours Accidents Adjusted accident
287287 4 3.843
270828 8 8.228
298531 4 3.630
271726 4 4.149
280771 7 6.961
282547 9 8.905
226415 18 20.685
226410 2 2.917
253482 2 2.429
270376 4 4.176
283216 15 14.843
278348 5 5.018
296736 5 4.633
308166 19 17.731
298507 9 8.466
295858 5 4.651
307692 5 4.414
273973 4 4.104
293849 4 3.718
Analysis was performed using adjusted accident with UCL=16.794, Avg=7.000, LCL=1.206
Ed,
Without reading the article, I don’t know what is intended by these terms.
Charles
Charles,
Please follow the link below for details.
http://www.aptleadership.com/performance-improvement/software/data-analysis-software.html
Thanks.
Ed
Charles,
I still can’t figure out how the author “uses standard statistical theory to adjust the number of accidents based on the variation of the man-hours worked from month to month.”
Any help is much appreciated.
Thanks.
Ed
Sorry Ed, but I haven’t had time to look into to this further. Have you been able to figure out what the author did?
Charles
Hy Charles..
I have to make an assignment on “fitting a poison distribution to observed data”
So tell me how many numbres of data will be suitable. ???
I shall be
very thankful to you.
Zarish,
Sorry, but I don’t know how many numbers is suitable. In fact, first you need to define what “suitable” means.
Perhaps someone else has some insight into this issue.
Charles
Hi.
How can I calculate this:
A fire brigade A is on average called out 5 times a day. 1 call takes on 1hour for the brigade. a) What is the probability that the men can rest at least 2 hours between the calls. b) What is the probability that the brigade B has to be sent out because the brigade A is still on its duty.
The answes should be a) 0.535 and b) 0.188
I would be really glad if you could help me…
Sorry Anti, but this looks like a school assignment and I don’t want to answer such questions. I am happy to clarify concepts, but not provide such specific answers.
Charles
Sir, I have 12 data sets how to check distribution on these data sets?
To check for normal distribution, see Testing for Normality
Also see
Goodness of Fit
KS Test
Charles
Hi Charles,
I am doing a project on diagnostic errors in medicine. I want to show the number of errors per month over a 6 month period. Overall, for 200 events I have about 150 with errors and 50 without errors. How do I use poisson distribution in this case? I do know in each month how many errors occur. Do we need this data? I am using Excel, so what will be the formula?
Mayukh,
You know that the probability of an error is 3/4. Now you need to know how many events occur in a month, and from this it is easy to calculate the average number of errors per month. If however you want to know the probability that you will have say m errors in the month (instead of the average number), then you can use the approach described on the referenced webpage.
Charles
If a cumulative probability distribution function is the probability that a random variable will have a value less than or equal to X, what would be the function name for the opposite(he probability that a random variable will have a value grater than or equal to X, or even just greater than X)?
It depends on the context. For example, in survival analysis this is called the survival function.
Charles
Say a user can check out a maximum of 2000 licenses at a time. Multiple users can check out one or more licenses each hour for a product but not more than 2000. The product owner has log that shows data for each hour in the year (365 days). For each hour, the log contains the highest number (quantity) of licenses checked out in that hour. Using this log of every hour over the past year, how would you determine for the next year if 2000 licenses is enough based on this data using a Poisson distribution function in excel? What would be the average be? Note that in many cases, the licenses checked out one hour is the same licenses check out by the same person in a previous hour(the license continues to be check out by the same user over multiple hours or days). Do you believe this is a Poisson Distribution? Also, how would you calculate the mean?
Able,
Please explain the premise more clearly. If a user checks out 2,000 in one hour, can he/she check out another 2,000 licenses in the next hour? (i.e. are these like checking out books in a library?) If you have say 10 users can they each check out 2,000 licenses in an hour (for a total of 20,000 licenses) or are they restricted to 2,000 licenses in aggregate?
What criterion are you using for determining whether “2000 licenses is enough based on this data using a Poisson distribution function in excel?” Do you mean that (1) in no hour is more than 2,000 licenses checked out or (2) the probability of more than 2,000 licenses being checked out is zero or (3) something else?
Charles
Charles,
In response to you comments:
1)If a user checks out 2000 licences one hour, in the next hour either their will be 0 licenses checkout out or the same 2000 licenses that were checked out in the previous hour(s). It all depends if a users software job has ended or not and the user does not require any more licenses.
2)If you have 10 users they are they restricted to 2,000 licenses in aggregate per hour.
3)I am looking for probability of more than 2,000 licenses being checked out is zero. I am also looking for the lowest license count where the probability of more than x number licenses being in use is 0.
It appears that you are assuming an “arrival time” (i.e. checking out of licenses) that follows a Poisson distribution, but you haven’t said anything about the “service time” (i.e. for how long the license is checked out). If we assume, for example that the arrival time follows a Poisson distribution with mean m and a service time whose average is say n, then we have a typical queueing model.
Is this is what you are interested in?
Charles
Charles,
I do not have information regarding the service time, just the arrival time. Can Poisson or perhaps another statistical method be used to determine the probability of more than 2,000 licenses being checked out is zero with just the arrival time information?
Charles, May I ask you a question about Poisson function on excel ? what would be the best way to ask you?
You can ask as a Comment.
Charles
say i have a sign up rate of about 2 per day
and each signup lasts for exactly 30 days
what is the probability that I will have at least a hundred people signed up at once?
Assuming that you are looking for the probability that at least 100 people are signed up in any specific 30 day period, then the result should be =1-POISSON.DIST(99,60,TRUE), which has a value of 1.48E-06, a very small number.
Charles
Hi.May I ask a question?
When n (from 5 to 10 and 20)increases what happens on the probability distribution graph?(binomial, poisson and normal)
It really depends on what happens with the other parameters.
Binomial: If the other parameters in the BINOMDIST function are held constant then the cumulative distribution values decrease (e.g. compare BINOMDIST(4,n,.7,TRUE) for n = 5, 10, 20.
Poisson: If you assume that the mean of the distribution = np, then the cumulative distribution values decrease (e.g. compare POISSON(2,np,TRUE) where p = .5 for n = 5, 10, 20.
Normal: It really depends on how you are going to use n since NORMDIST doesn’t directly use n.
Charles
Hi Charles,
Many thanks for the explanation, i’m trying to find a way to apply this to sports betting using Excel, i’ve managed to locate a Poisson template and i’m wondering if there are any know ways of viewing football prediction results
I don’t know any way of applying this to sports betting, but perhaps someone else in the community can help.
Charles
Hi Charles,
I wonder if it would be correct to use poisson distribution to determine safety stock for a product when the product has the following demand pattern for the last 12 months:
3 580
0
0
1 135
1 000
363
2 175
72
620
92
228
373
The reason behind this pattern is that one of the customers is buying given product in batches.
Thank you in advance.
Alice,
I have just updated the Chi-square Goodness of Fit webpage with a test to determine whether data conforms to the Poisson distribution. This can be found at the bottom of the https://real-statistics.com/chi-square-and-f-distributions/goodness-of-fit/ webpage, and should be helpful in answering your question.
Charles
Excellent resource!
I have used it to sucessfully simulate a poisson process (counts of a radioactive material) and has helped me to make a worksheet to obtain detection tresholds and minimun detectable activity (they are dependant of sigma) for the contaminations sensors i use.
Keep the good work!
The average number of signals sent from a station is 3 per day which do not reach properly to the another station . Find the probability that the signals which are sent in a day but not reached properly is at least 3
Please help me to solve this problem ….thanks in advance
1-POISSON(2,3,TRUE) assuming a Poisson distribution.
Charles
https://real-statistics.com/binomial-and-related-distributions/poisson-distribution/
Typo: the setup for the question stipulates a 0.05% probability of occurrence and the calculated result agrees with that. However, the formula as shown below appears to use 0.06% [.0006] rather than 0.05%. Just a typo; the result is based on the .05% value.
1 – BINOMDIST(3, 4000, .0006, TRUE) = 1 – 0.857169 = 0.142831
Greg,
Yes, you are correct. Thanks for catching this typo. I have now corrected it on the referenced webpage.
Charles