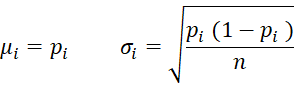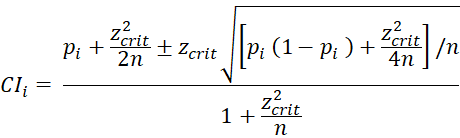Proportional Multivariate Distribution

Definition 1: For an experiment as described in Definition 1 of Multinomial Distribution, let x₁, x₂, …, x_k be discrete random variables whose values are the proportion of times outcome E_i occurs in n trials. Then x₁, x₂, …, x_k have a proportional multinomial distribution. The (joint) probability density function g is defined as follows:

g(x₁, x₂, …, x_k) = f(nx₁, nx₂, …, nx_k)

where f is the pdf for the multinomial distribution, as defined in Definition 1 of Multinomial Distribution.

Mean and Standard Deviation

By Property 1 of Proportion Distribution, for each i, the expected proportion of times outcome E_i occurs in n trials and the standard deviation of this mean are given by

Confidence Interval

For any sample of size n, if p_i is the proportion of the times outcome E_i occurs in n trials, then the following is an estimate for the 1–α confidence interval for the population mean μ_i using a normal distribution approximation:

where z_crit is the critical value of the standard normal distribution, i.e.

z_crit = NORM.S.INV(1– α/2)

Note that this calculation of the confidence interval (due to Edwin Wilson) is an improvement of the version described in Proportion Distribution, namely

In fact, this version can also be used with the proportional (binomial) distribution.

References

Wikipedia (2023) Binomial proportion confidence interval
https://en.wikipedia.org/wiki/Binomial_proportion_confidence_interval#Wilson_score_interval

Wilson, E. B. (1927) Probable inference, the law of succession, and statistical inference
http://www.med.mcgill.ca/epidemiology/hanley/bios601/Proportion/wilson_jasa_1927.pdf