Dirichlet Distribution

Basic Concepts

The Dirichlet distribution is a generalization of the beta distribution in the same way as the multinomial distribution is a generalization of the binomial distribution. First, note that

The multivariate version of the beta function for α = (α₁, …, α_k) where α_i > 0 for each i, is

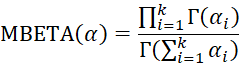
The pdf of the beta distribution is

The pdf of the Dirichlet distribution at P = (p₁, …, p_k), where and p_i > 0 for all i, is

Properties

Figure 1 shows key properties of this distribution where γ = and μ_i = α_i/γ for each i

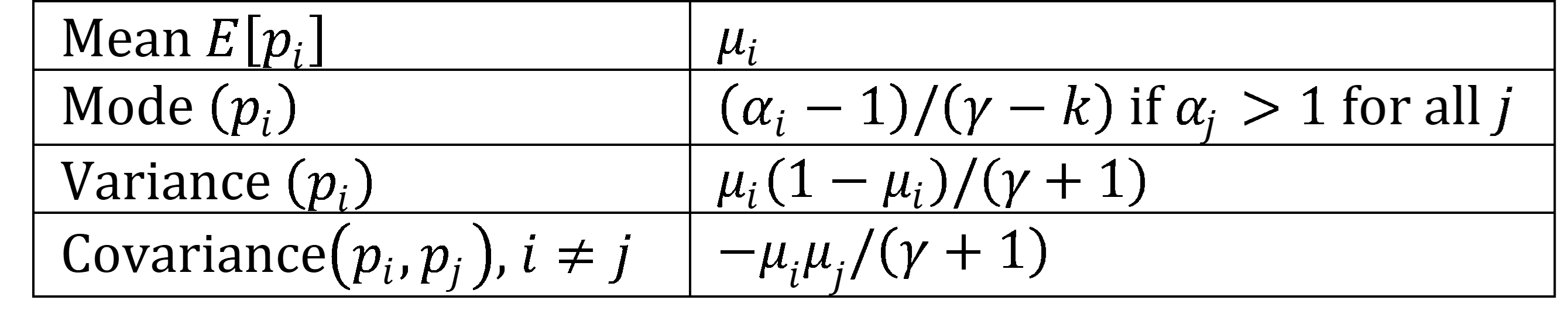
Figure 1 – Dirichlet distribution properties

Note too that the marginal distribution at p_i is p_i ∼ Bet(α_i, 1–α_i).

To draw a random vector (p₁,…, p_k) from the Dirichlet distribution, follow the following steps using the gamma distribution:

1. For each i = 1, …, k, draw a random value z_i ∼ Gamma(α_i, 1) using the formula =GAMMA.INV(RAND(), α_i, 1)
2. For each i, set p_i = z_i /

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack supports the following functions. Here, R1 is a row or column array containing non-negative p_i values that sum up to 1 and R2 is a row or column array containing positive values.

DIRICHLET_DIST(R1, R2) = value of the pdf of the Dirichlet distribution at R1 using the alpha values in R2 where R1 and R2 have the same shape and size.

DIRICHLET_RAND(R2): array function that outputs a random row or column array from the Dirichlet distribution with alpha values in R2: the array that is output has the same size and shape as R2.

MBETA(R2) = multivariate version of the beta function on the alpha values in R2

References

Wikipedia (2020) Dirichlet distribution
https://en.wikipedia.org/wiki/Dirichlet_distribution

Frigyik, B. A., Kapila, A., Gupta, M. R. (2010) Introduction to the Dirichlet distribution and related processes
https://vannevar.ece.uw.edu/techsite/papers/refer/UWEETR-2010-0006.html