Property 0: B(n, p) is a valid probability distribution
Proof: the main thing that needs to be proven is that
where f(x) is the pdf of B(n, p). This follows from the well-known Binomial Theorem since
The Binomial Theorem that
can be proven by induction on n.
Property 1
![]()
Proof (mean): First we observe
Now
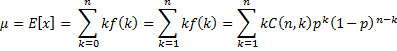
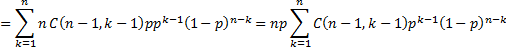
where m = n − 1 and i = k − 1 . But
where fm,p(i) is the pdf for B(m, p), and so we conclude μ = E[x] = np.
Proof (variance):
We begin using the same approach as in the proof of the mean:
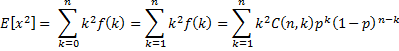
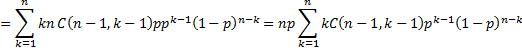
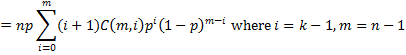

![]()
Thus,
![]() References
References
Hoel, P. (1962) Introduction to mathematical statistics, 3rd Ed. John Wiley and Sons
ProofWiki (2021) Expectation of binomial distribution
https://proofwiki.org/wiki/Expectation_of_Binomial_Distribution
ProofWiki (2021) Variance of binomial distribution
https://proofwiki.org/wiki/Variance_of_Binomial_Distribution
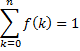
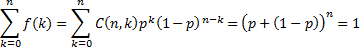



Two points in the variance proof are not clear. Why does the probability function sum up to one when the parameter C(m,i+1) is used instead of C(m,i) as in:
SUM(i=0,m){C(m,i+1)p^i(1-p)^m-i
Second, Why does the following sum equal to mp when the “i” is part of the multiplicand?
SUM(i=0,m){i*C(m,i+1)p^i(1-p)^m-i}. I am not familiar with this identity. Thanks!
Robert,
The proofs that were given were not quite right. I have now made a some corrections which should address the issues that you raised. Thanks for bringing these to light.
Charles