We start by considering the following problem and then show how it relates to the binomial distribution.
Example 1: Suppose you start at point 0 and walk either one unit to the right or one unit to the left, where there is a 50-50 chance of either choice. Now repeat this process 100 times. What is your expected distance from the starting point?
Basic Concepts
This is a simple form of what is called a random walk problem. Define the random variables xi as follows:
Now let dn = your distance from the starting point after the nth trial. Thus
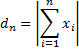
To solve Example 1 we need to find the expected value E[d100]. We accomplish this by using Properties 1 and 2.
Properties
Property 1: If x ∼ N(0, σ2), then
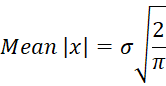
Proof: See proof of Property 5 of Advanced Properties of Probability Distributions.
Property 2: For n sufficiently large
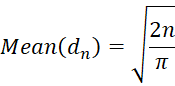
Proof: Let {x1, …, xn} be a random walk for x = . First we note that the mean of each xi is (.5(1) + .5(-1))/2 = 0 and the variance is ((1-0)2 +(-1-0)2)/2 = 1; i.e. xi ∼ N(0, 1).
The random walk can therefore be considered to be a random sample from a standard normal distribution, and so by Corollary 1 of the Central Limit Theorem, for n sufficiently large, the sample mean of x is approximately normally distributed with mean 0 and standard deviation 1/. But the sample mean of x is
. Thus
By Property 1 of Basic Characteristics of the Normal Distribution, it follows that
and so by Property 1
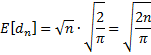 Examples
Examples
Example 1 (continued): We can now use Property 2 to complete Example 1, as follows:
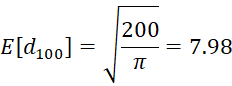
and so we see that on average your distance from the starting point is just under 8 units. Sometimes you end up to the right of the starting point and sometimes you end up to the left of the starting point (and sometimes, although far less often, you end up right back at the starting point).
Example 2: Suppose you toss a fair coin 100 times. By Property 1 of Binomial Distribution, the average number of heads is 100(.5) = 50 and the average number of tails is 50. But we know that 100 tosses won’t always result in 50 heads and 50 tails. So on average how many more or fewer heads are there than the average of 50?
It is easy to see that the answer to this question is the average value of |# of heads – 50|. But what is this value?
If we view getting heads as going right and getting tails as going left in our random walk problem, we see that the solution to this example is also E[d100]. In general, the average number of heads after n tosses is n/2 and so
the average value of |# of heads after n tosses – n/2| = E[dn]
Since
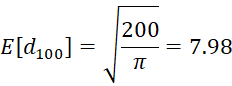
we see that the answer to Example 2 is again just under 8. In fact, this means that not only is it not necessarily the case that heads and tails break 50-50 in 100 tosses but on average heads are 8 units away from 50, i.e. on average, heads and tails break 58-42 (although not necessarily is the 58 for heads).
Observation
Note that for any a and b, |a| < b is equivalent to –a < b < a. Since, as we have seen above, ~ N(0,n), it follows that the probability that dn = |
| < k for any value of k is NORM.DIST(k, 0, SQRT(n), TRUE) – NORM.DIST(-k, 0, SQRT(n), TRUE) = 2*NORM.DIST(k, 0, SQRT(n), TRUE)–1.
For example, P(d100 < 7) = .758 – .242 = .516.
References
Hoel, P. (1962) Introduction to mathematical statistics, 3rd Ed. John Wiley and Sons
Tijms, H. (2007) Understanding probability: chance rules in everyday life (2nd ed.). Cambridge: Cambridge University Press.
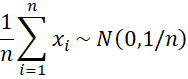
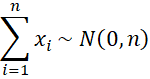
How do you solve this problem. A coin is tossed 7 times. Your beginning position is at zero. If you get heads you go right one unit from zero. If you get tails you go left one unit. What is the probability that you will return to zero at least once?
Pete,
I am sure that you can solve this problem in the same way, but here is a straighforward approach:
1. It doesn’t matter which direction you go on the first toss and so I will assume it is left L. Note too that it doesn’t matter what direction you go on the 7th toss. Also after 4 lefts you can’t succeed.
2. The only sequences that are successful are LR, LLRR, LLLRRR, LLRLRR
3. The probabilities of these 1/2, 1/8, 1/32, 1/32, for a total of 11/16.
Charles
Hi Charles
I am still unable to build up the connections between average value of |# of heads – 50| and E[dn]. Could you explain more specifically how they match up?
As you pointed out that if we let x be the random variable which takes the value 1 if heads is thrown and -1 if tails is thrown, then one step random walk is a Bernoulli trail and 100-time repetitions generate binomial distribution in the first place, so why do we need all those coin tossing stories?
Jeff,
d_100 = the distance from the origin that you arrive at after 100 random walks (going left has a 50% probability and going right has a 50% probability). But it also turns out that d_100 = the number of heads – 50 after 100 tosses (getting heads has 50% probability and getting tails has a 50% probability), assuming more heads than tails are tossed. You can think of heads as equivalent to going right and tails as equivalent to going left,
Charles
Hi! I know for a random walk, at least in a 2 dimensional space, with a constant “step” length and ANY direction possible the expected “stray” from the starting point is directly proportional to the square root of the number of steps taken. My question is this: what is the Distribution of distances strayed from the starting point for this model?
Robert,
I don’t know what the distribution is. The webpage gives the mean of the distribution. Perhaps the following webpage gives more info:
http://mathworld.wolfram.com/RandomWalk1-Dimensional.html
Charles
Hi Charles,
This is great. Thank you for putting this great resource together. However, the link “By Property 5 of Properties of Distributions Detailed (the proof of which uses calculus)” is not returning the desired page. Please can you fix it. I am really keen to see a neat proof of this.
Thanks & Regards
Prab
Hi Prab,
I have now repaired the broken link. Thanks for catching this problem.
Charles
This awesome, Thank you!!