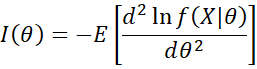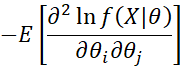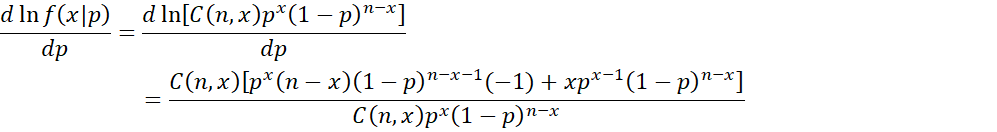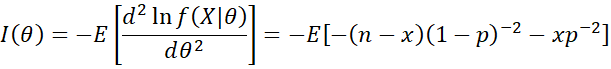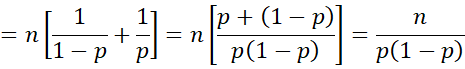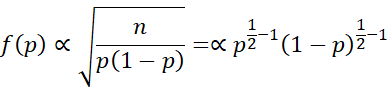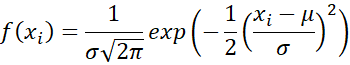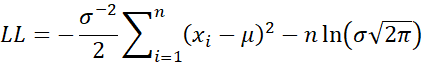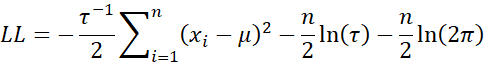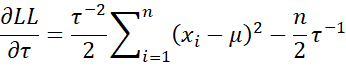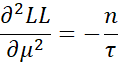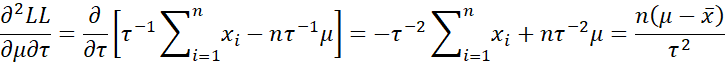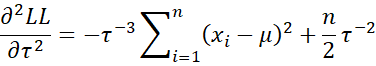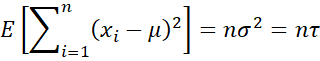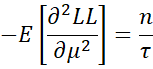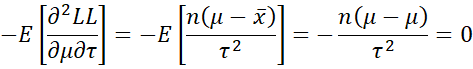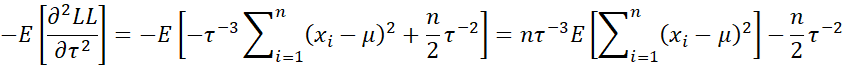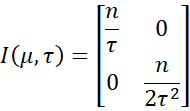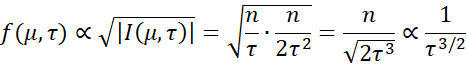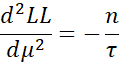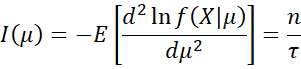Jeffreys’ Priors

Basic Concepts

A commonly used non-informative prior is Jeffreys’ prior, which for parameter θ is defined as

where

and the expectation is with respect to X|θ.

Jeffreys’ prior for multivariate parameters θ = (θ₁, …, θ_k) is defined as

where I(θ) is a k × k matrix whose (i, j) element is

Binomial data

Suppose x ~ Binom(n, p), and so f(x|p) = C(n, x)p^x(1–p)^n–x. We assume that n is fixed. Thus

Since E[x] = np for a binomial distribution, it follows that

It follows that Jeffreys’ prior is

which is the kernel of Bet(1/2,1/2), the non-informative prior described at Beta Conjugate Prior.

Normally distributed data

Suppose x₁, …, x_n are data from the distribution N(μ,σ²). The pdf for each x_i is

Thus

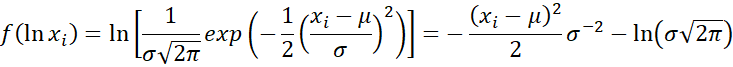
It now follows that

Setting τ = σ², it follows that

We now calculate the first partial derivatives.

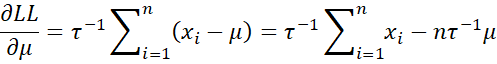
The second partial derivatives are as follows:

Note that

Hence, we have the following three expected values:

Thus

And so, Jeffreys’ prior can be expressed as

From which it follows that

Normally distributed data with fixed variance

As we saw above

Thus

And so Jeffreys’ prior is

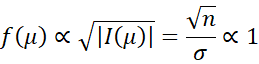
which is an improper prior.

References

Reich, B. J., Ghosh, S. K. (2019) Bayesian statistics methods. CRC Press

Lee, P. M. (2012) Bayesian statistics an introduction. 4^th Ed. Wiley
https://www.wiley.com/en-us/Bayesian+Statistics%3A+An+Introduction%2C+4th+Edition-p-9781118332573

Jordan, M. (2010) Bayesian modeling and inference. Lecture 1. Course notes
https://people.eecs.berkeley.edu/~jordan/courses/260-spring10/lectures/lecture1.pdf

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., Rubin, D. B. (2014) Bayesian data analysis, 3^rd Ed. CRC Press
https://statisticalsupportandresearch.files.wordpress.com/2017/11/bayesian_data_analysis.pdf