Basic Concepts
When the prior and posterior distributions are both from the same distribution family then we say that the pair is conjugate. These conjugate pairs are based on some distribution of the data. E.g. we refer to an exponential-gamma system when the data is an independent random sample from an exponential distribution where both the prior and posterior of the exponential distribution parameter are the pdf of a gamma distribution.
When the distribution of the data has multiple parameters, we also need to specify which of the parameters are known (and so can be treated as constants) and which are unknown (and so require prior and posterior distributions).
Exponential-Gamma
Property 1: If the independent sample data X = x1, …, xn follow an exponential distribution (and so xi ≥ 0 for each i) with an unknown rate parameter λ with a prior gamma distribution of λ ∼ Gamma(α, β) then the posterior distribution is λ|X ∼ Gamma(α′, β′) where
Proof: Note first that λ > 0, which is compatible with a gamma distribution. Since the prior follows a gamma distribution, we know that the pdf is
Since the likelihood function is the product of exponential pdf functions
It follows by Bayes Theorem that
![]()
which completes the proof since this last formula is proportional to the pdf of the specified gamma distribution.
Poisson-Gamma
Property 2: If the independent sample data X = x1, …, xn follow a Poisson Distribution (and so xi ≥ 0 for each i) with an unknown mean parameter with a prior gamma distribution of λ ∼ Gamma(α, β) then the posterior distribution is λ|X ∼ Gamma(α′, β′) where
and
Proof: We proceed as in the proof of Property 1.

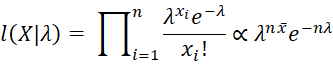
![]()
![]()
Since f(λ|X) is proportional to the pdf of Gamma(α′, β′), this completes the proof.
Example 1: As described in Example 2 of Poisson Distribution, radioactive particles hitting a screen follow a Poisson distribution. We observe that 200 radioactive particles hit a screen in the past 300 seconds. Using a prior gamma distribution with a mean of .75 and standard deviation of 1 for lambda, the mean of the Poisson distribution, what is the posterior distribution for lambda?
Since λ ∼ Gamma(α, β), we know that
mean = αβ = .75
variance = αβ2 = 1.0
Thus, 1.0 = αβ2 = .75β, and so β = 4/3 = 1.3333 and α = .75/(4/3) = 9/16 = .5625.
By Property 2, the posterior distribution λ|X ∼ Gamma(α′, β′) where
from which the posterior mean and standard deviation can be calculated
This means that the estimated value for lambda is now .6669 with a standard deviation much lower than the previous standard deviation of 1.


