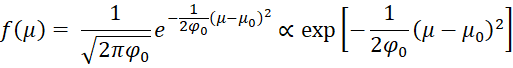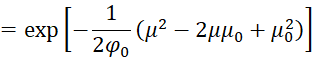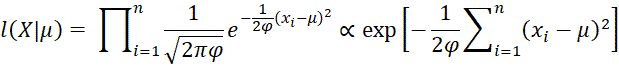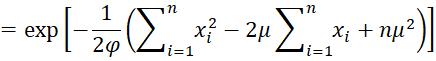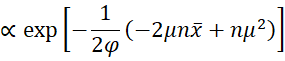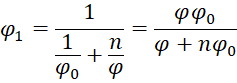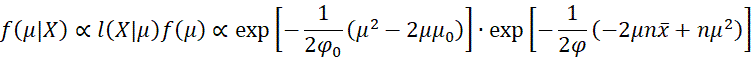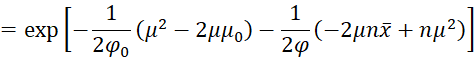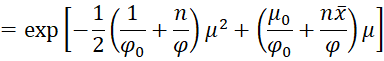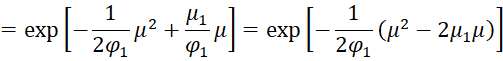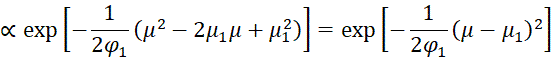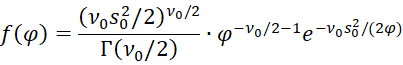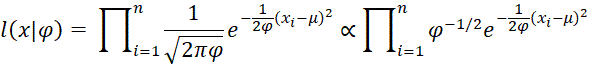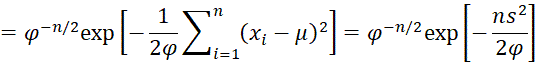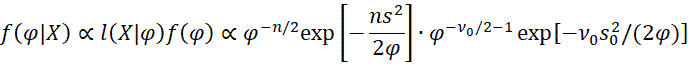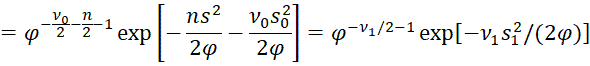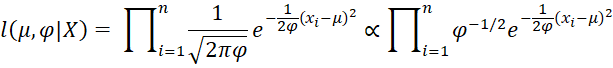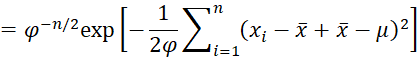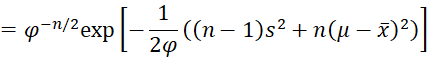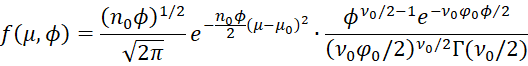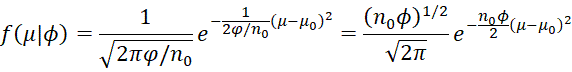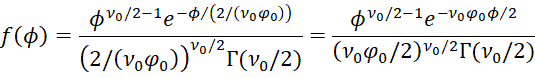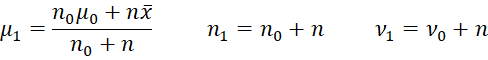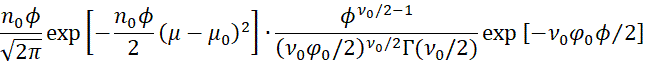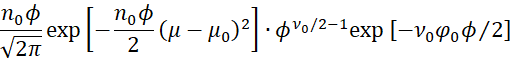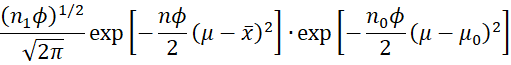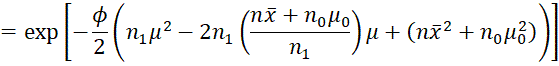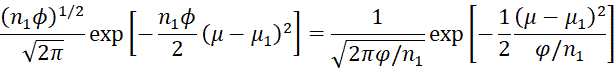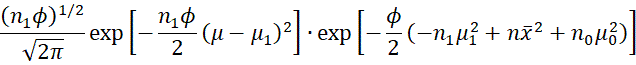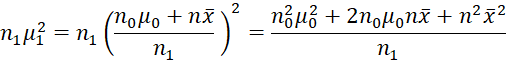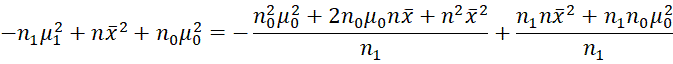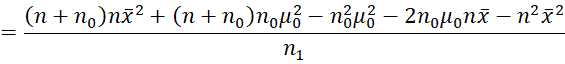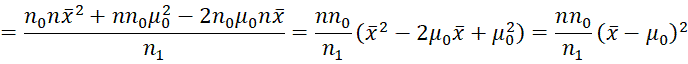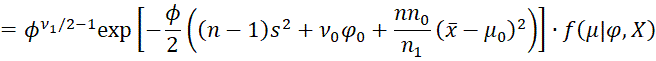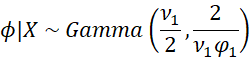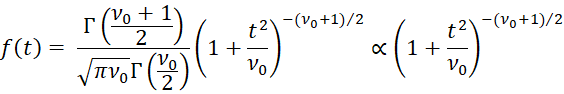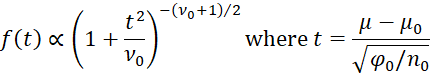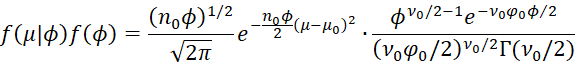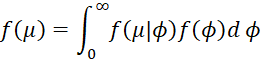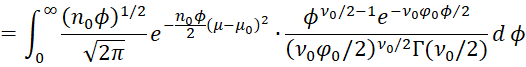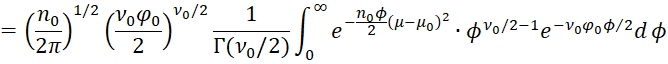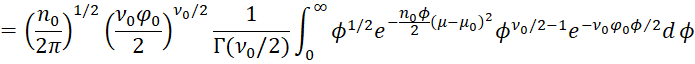Normal Conjugate Priors Proofs

Unknown mean and known variance

Property 1: If the independent sample data X = x₁, …, x_n follows a normal distribution with a known variance φ and unknown mean µ where X|µ ∼ N(µ, φ) and the prior distribution is µ ∼ N(µ₀, φ₀), then the posterior µ|X ∼ N(µ₁, φ₁) where

Proof: Note that in the proof the proportionality symbol ∝ is used when the previous term is multiplied by a value that doesn’t involve μ, especially when a term not involving µ is added or removed from the expression inside exp.

The prior distribution of the mean parameter is

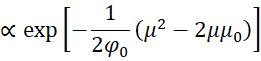The likelihood function is

Using the following equivalence

and Bayes Theorem it follows that

This completes the proof since this last formula is proportional to the pdf of the required normal distribution.

Unknown variance and known mean

Property 2: If the independent sample data X = x₁, …, x_n follow a normal distribution with an unknown variance φ and a known mean µ where X|φ ∼ N(µ, φ) and the prior distribution is φ ∼ Scaled-Inv-χ²(ν, s₀²) with scale parameter s₀² and degrees of freedom ν₁ > 0, then the posterior φ|X ∼ Scaled-Inv-χ²(ν₁, s₁²) where

Proof: The prior distribution of φ is

The likelihood function is

By Bayes Theorem

This completes the proof since this last expression is proportional to the pdf of the required scaled inverse chi-square distribution.

Unknown mean and variance

Property A: If the independent sample data X = x₁, …, x_n follow a normal distribution with an unknown mean µ and variance φ where X|µ, φ ∼ N(µ, φ), then the likelihood function can be expressed as

where ϕ = 1/φ

Proof:

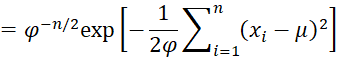
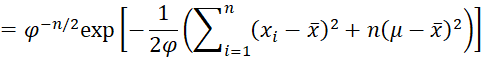
Since ϕ = 1/φ, it follows that

which is equivalent to the desired result.

Property B: If μ, ϕ has a normal-gamma distribution

then the joint probability function can be expressed as

Proof: The conditional probability of μ can be expressed as

Since the marginal probability of ϕ is

we see that the joint probability is

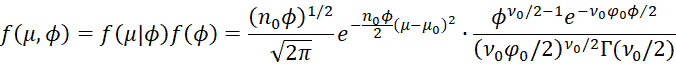
Property 3: If the independent sample data X = x₁, …, x_n follow a normal distribution with an unknown mean µ and variance φ where X|µ, φ ∼ N(µ, φ) and

with ϕ = 1/φ, then the posterior is

where

Proof: Using Properties A and B

Here, we have removed multipliers not involving μ, ϕ from the fourth term in the product and added a multiplier not involving μ, ϕ to the second term. Reordering the terms and using the fact that n₁ = n₀ + n, yields the following:

Here, the last two terms involve μ, while the first two terms don’t involve μ.

We can reorganize the terms that involve μ as follows:

Note that the first term involves μ, while the second term does not. Note too that

which is the pdf for N(μ₁, φ/n₁), i.e. f(μ|φ, X)

We can now substitute this result into the original expression for f(μ,φ|X), namely

But

and so

It now follows that

But the first term in the product represents the gamma pdf for ϕ|X since

is equivalent to

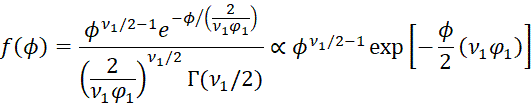
which completes the proof.

Property 4: If the independent sample data X = x₁, …, x_n follow a normal distribution with an unknown mean µ and variance φ where X|µ, φ ∼ N(µ, φ) and

with ϕ = 1/φ, then the marginal distribution of μ is

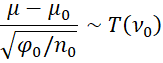
Proof: If t ∼ T(ν₀), then the pdf would be

Thus, it would be sufficient to show that

Let ϕ = 1/φ₀. Then, as we observed at the beginning of the proof of Property 3

and so

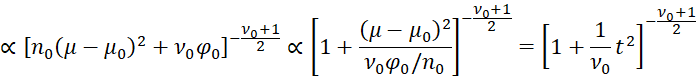
Property 5: Given the premises of Property 4, it follows that for ν₀ > 1, the mean of μ is μ₀

Proof: Let

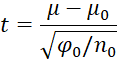
By Property 4, the mean of t is 0 for ν₀ > 1. Since

it follows that the mean of μ is

References

Clyde, M., Çetinkaya-Rundel M., Rundel, C., Banks, D., Chai, C., Huang, L. (2019) An introduction to Bayesian thinking
https://statswithr.github.io/book/inference-and-decision-making-with-multiple-parameters.html

Walsh, B. (2002) Introduction to Bayesian Analysis
http://staff.ustc.edu.cn/~jbs/Bayesian%20(1).pdf