Bayesian Example

On this webpage, we illustrate some of the concepts described in Introduction to Bayesian Statistics.

Example 1

The false-positive rate for an HIV test is 7% and the false-negative rate is 1%. If 0.148% of the population has HIV, what percentage of the population who test positive for HIV actually has HIV?

Let T = the test is positive (for HIV) and D = the subject has HIV disease. Thus

P(T|D′) = .07 (false positive rate)

P(T′|D) = .01 (false negative rate)

P(T′|D′) = 1-.07 = .93 (specificity)

P(T|D) = 1-.01 = .99 (sensitivity)

P(D) = .00148 (probability of disease)

By Bayes Theorem

from which it follows that

Example 2

Suppose that we test each subject three times and suppose further that each test is independent of the others (even though this assumption is quite dubious since it is highly likely that the results of a second test will be the same as that on the first test).

One way to handle this situation is to assume that the prior on the second test is the posterior on the first test, and similarly for the third test. 

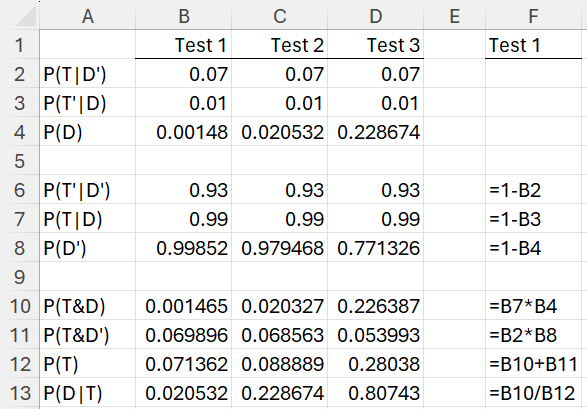
The results are shown in Figure 1. Column F also shows the formulas used in column B.

Figure 1 – Multiple tests

Cell E4 shows the posterior probability after one test (2.05% in cell B13). We use this value as the prior probability for the second test, as shown in cell C4, yielding a posterior of 22.87% (cell C13). This process is repeated one more time, yielding a posterior probability of 80.74% (cell D13).

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Sun, D. (2020) Bayes’ Theorem. Github
https://dlsun.github.io/probability/bayes.html