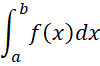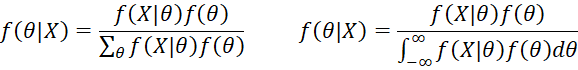Objective
Bayesian statistics uses an approach whereby beliefs are updated based on data that has been collected. This can be an iterative process, whereby a prior belief is replaced by a posterior belief based on additional data, after which the posterior belief becomes a new prior belief to be refined based on even more data. The initial prior belief in this series may be based on intuition, previous studies, experience, etc.
In inferential statistics, we commonly test hypotheses, estimate parameters, and make predictions. The traditional approach to statistics, commonly called the frequentist approach, views parameters as constants whose values we aim to discern. In the Bayesian approach, we treat these parameters instead as variables that have a probability distribution.
Assumptions for the Reader
For the most part, we assume that the reader has some familiarity with the frequentist approach, as described in the rest of this website, although some concepts will be re-examined.
We don’t assume, however, that the reader is familiar with calculus. This is easier to do in frequentist statistics, where we can avoid the details of Newton’s method and maximization techniques, which rely on calculus, confining these details to an appendix for those who are interested and have the appropriate background.
In Bayesian statistics, we are constantly referring to an integral, which is one of the bedrock concepts in calculus. We will use integral expressions such as
but you can view this expression as representing a summation
where Δx is a small positive value and n = (b–a)/Δx. We get better and better estimations for the integral the smaller the value of Δx that is used.
Bayes Theorem
The simple form of Bayes Theorem (aka Bayes Rule or Bayes Law) is
If A1, A2, …, Ak partition the sample space S (i.e. S = A1 ∪ A2 ∪ … ∪ Ak and Ai ∩ Aj = ∅ for i ≠ j) then
which is called the Law of Total Probability, as described in Basic Probability Concepts.
Combining the above two formulas, we get
In terms of probability functions, Bayes Theorem can take one of the following forms:
where the equation on the left is used in the discrete case and the equation on the right is used in the continuous case.
Parameter Estimation
More specifically, suppose that θ is one or more parameters that we are trying to estimate. Since we are using a Bayesian approach, we consider θ to be a variable (or variables) that has a probability distribution. The prior distribution (i.e. the distribution before we collect any data X) has a probability distribution function (pdf) f(θ), while the posterior distribution (i.e. the distribution after we have collected data X) has a pdf f(θ|X).
f(X|θ) is the likelihood function, which can be considered to be a function l(θ|X) of θ conditional on the data X. The denominator of the above formulas is called the evidence, where, in the discrete case, the summation is over all possible values of θ (note that θ in the numerator refers to only one such value of θ), while in the continuous case an integral plays the same role as the summation.
Thus, Bayes Theorem provides a way to express the posterior pdf in terms of the likelihood function and the prior pdf. Quite often it will be convenient to express this equation as a proportion
where the proportionality factor is
i.e. f(θ|X) = kf(X|θ)f(θ) = kl(θ|X)f(θ). Often the proportionality factor may not be easy to calculate (especially in the continuous case). The proportion expression of Bayes Theorem shifts attention away from the proportionality factor, but since f(θ|X) is a pdf, we may be able to figure out the value of f(θ|X) without having to directly calculate the proportionality factor. Often, however, it will be necessary to use special techniques, such as Markov Chain Monte Carlo (MCMC), to estimate the proportionality factor.
References
Lee, P. M. (2012) Bayesian statistics an introduction. 4th Ed. Wiley
https://www.wiley.com/en-us/Bayesian+Statistics%3A+An+Introduction%2C+4th+Edition-p-9781118332573
Jordan, M. (2010) Bayesian modeling and inference. Lecture 1. Course notes
https://people.eecs.berkeley.edu/~jordan/courses/260-spring10/lectures/lecture1.pdf
Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., Rubin, D. B. (2014) Bayesian data analysis, 3rd Ed. CRC Press
https://statisticalsupportandresearch.files.wordpress.com/2017/11/bayesian_data_analysis.pdf