Basic Concepts
One way to determine the sample size required is to run the Metropolis algorithm a few times with a different initial guess and see whether the resulting histograms look similar. Another approach is to investigate the autocorrelation at different lags and calculate an effective sample size (ESS), which attempts to factor out the effect of autocorrelation. If ACF(k) is the autocorrelation at lag k, then the effective sample size is
Since we can’t calculate an infinite sum, we usually carry out the sum up to the point where ACF(k) becomes small enough, say when ACF(k) < .05.
If we are using the Metropolis algorithm to determine a statistic that depends on the less dense parts of the distribution (e.g. the 95% HDI) then an ESS = 10,000 is typically sufficient. For a statistic that is based on the denser part of the distribution (e.g. the median), then the ESS can be much smaller.
Since the standard error of the mean for a random sample of size n is s/√n where s is the standard deviation of the sample, we can replace n by ESS to get the Markov chain standard error (MCSE):
where s is the standard deviation of the sample produced by the Metropolis algorithm. This statistic will give an estimate of the accuracy of the estimate of the mean of the distribution that is calculated by using the Metropolis algorithm.
Example
Example 1: Estimate the ESS and MCSE statistics for Example 1 of Metropolis Algorithm.
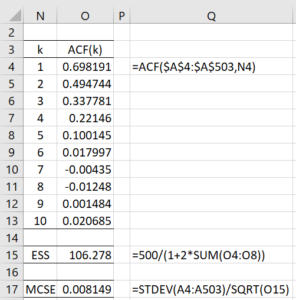
The results are shown in Figure 1.
Figure 1 – Estimates of ESS and MCSE
Here, we are using the Real Statistics ACF function to calculate the autocorrelation values at the first 10 lags. We see that these values get sufficiently close to zero at lag 6. We also see that the effective size of our sample is 106, which is quite small, and so we should have limited expectations of the accuracy of our results.
Worksheet Function
Real Statistics Function: The Real Statistics Resource Pack supplies the following array function that calculates the effective sample size.
ESS(R1, cutoff) = the effective sample size for the sample in R1 produced by the Metropolis algorithm; the ACF values are summed while ACF(k) < cutoff (default .05)
We can get the results for Example 1 by using the array formula =ESS(A4:A503).