Creating a Grid using Real Statistics

The Real Statistics Creating a Grid for Bayesian Analysis data analysis tool can be used to create a grid such as the ones displayed in Figure 2 of Grid Estimation.

Set-up

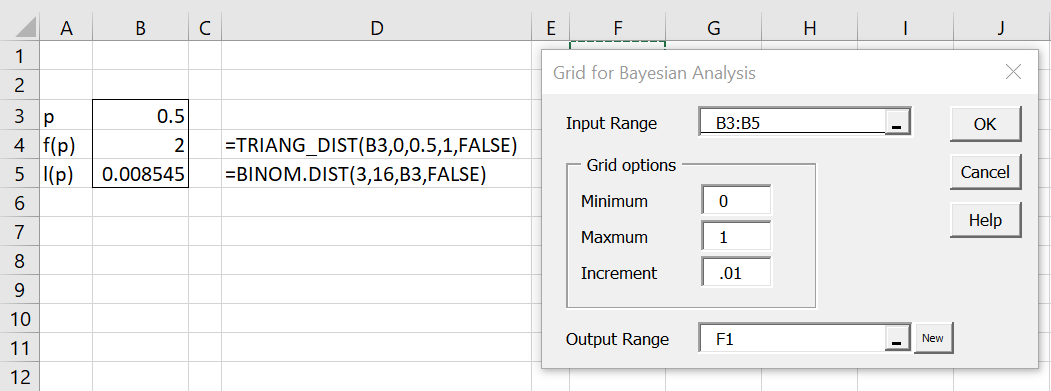
We now show how this is done for Example 1 of Grid Estimation. First, insert the formulas shown in range B3:B5 of Figure 1. Here, cell B3 represents the random variable, p in this case. You can enter any value in this cell since only the cell address, B3, will be used. The next cell, B4, contains the formula for computing the prior pdf at the value in cell B3. Actually, it is sufficient to use a formula for values that are proportional to the prior pdf. Finally, the last cell, B5, contains the formula for the likelihood function based on the parameter value in cell B3.

Real Statistics Data Analysis Tool

Now, press Ctrl-m, select the Creating a Grid for Bayesian Analysis option (from the Misc tab if using the MultiPage user interface), and fill in the dialog box that appears as shown on the right side of Figure 1.

Figure 1 – Grid data analysis tool

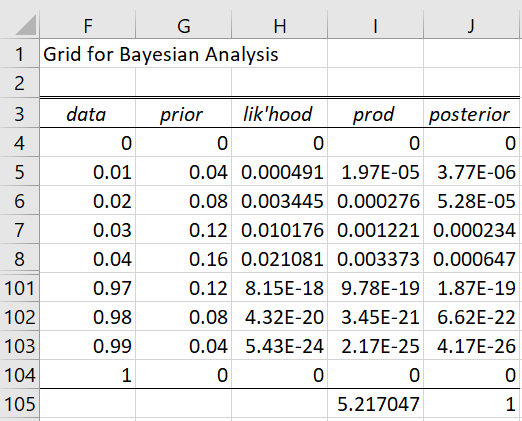
Upon pressing the OK button of the dialog box, the output is as shown in Figure 2 (although only the first and last few rows are displayed).

Output

Column F contains the values of p from 0 to 1 in increments of .01 (i.e. the values selected in the Minimum, Maximum, and Increment fields of the dialog box). Columns G and H contain the corresponding prior pdf and likelihood values. For example, cell G5 contains the worksheet formula =TRIANG_DIST(F6,0,0.5,1,FALSE) and H5 contains the worksheet formula =BINOM.DIST(3,16,F6,FALSE). These formulas are based on the formulas in cells B4 and B5.

Cell I5 contains =G5*H5 and cell J5 contains the corresponding estimated posterior pdf using the formula =I7/I$105 where cell I105 contains the formula =SUM(I4:I104). Note that even though the sum of the values of the cells in column G doesn’t add up to one, we get the correct posterior pdf estimates in column J.

Figure 2 – Grid

Click here for details on how to calculate the 95% high-density interval (HDI) for the posterior distribution in Figure 2 using Real Statistics.

Reference

Kruschke, J. K. (2015) Doing Bayesian data analysis. 2nd Ed. Elsevier
https://sites.google.com/site/doingbayesiandataanalysis/