We see from Figure 1 of Two Sample Binomial Metropolis Algorithm that more than half the time, the proposed value for (p, q) is rejected. This means that convergence will be quite slow. We now present another algorithm, called Gibbs Sampler, which will tend to converge to a solution more quickly. This algorithm can only be used when the required conditional probabilities are known.
Suppose we want a sample from the joint distribution f(θ, φ), but we don’t have access to this distribution directly, although we do have access to the distributions for θ|φ and φ|θ. In this case, we can use the following iteration method, called Gibbs Sampler.
- Start with a guess θ0 (which is any permissible value for θ)
- For each i > 0, get sample values θi ∼ f(θ|φi-1) and φi ∼ f(φ|θi)
Then for sufficiently large i, (θi, φi) ∼ f(θ, φ).
Example 1: Repeat Example 1 of Two Binomial Samples Beta Prior using Gibbs Sampler.
We want to sample from the posterior distribution for f(p, q|x, y). We can use Gibbs Sampler since the conditional probabilities are known, namely, by Property 1 of Beta Conjugate Prior
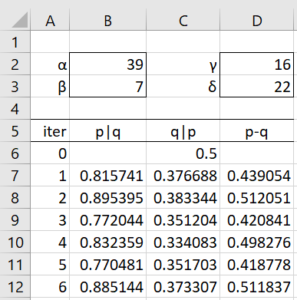
f(p|q, x, y) = f(p|x) ∼ Bet(39, 7) f(q|p, x, y) = f(q|y) ∼ Bet(16, 22)
Thus, we can use Gibbs Sampler as shown in Figure 1. This is a rather trivial use of Gibbs Sampler since at each iterative step, p doesn’t depend q and q doesn’t depend on p.
Figure 1 – Gibbs Sampler
Here, cell B7 contains the formula =BETA.INV(RAND(),$B$2,$B$3,FALSE) and cell C7 contains the formula =BETA.INV(RAND(),$D$2,$D$3,FALSE). All 500 values of p–q are positive, again supporting the hypothesis that the drug is effective.
Very Good