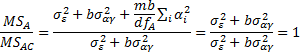Two within-subjects model| Real Statistics Using Excel

We now describe the structural model for repeated measures ANOVA where there are two within-subjects factors.

Definitions

Definition 1: We modify the structural model of Definition 1 of Two Factor ANOVA with Replication as follows. Note that we will use a to indicate the number of levels for factor A (instead of r) and b to indicate the number of levels for factor B (instead of c). Also, m = the number of subjects or participants.

We use terms such as x̄_i (or x̄_i.) as an abbreviation for the mean of {x_ijk: 1 ≤ j ≤ b, 1 ≤ k ≤ m}. We also use terms such as x̄_j (or x̄_.j) as an abbreviation for the mean of {x_ijk: 1 ≤ i ≤ a, 1 ≤ k ≤ m}.

We define the effects α_i and β_j where

Similarly, we define a_i and b_j where

We use δ_ij for the effect of level i of factor A with level j of factor B, i.e. the interaction of level i of factor A and level j of factor B. Thus, δ_ij = μ_ij – μ_i – μ_j + μ. Similarly, we have

It is easy to show that

Finally, we can represent each element in the sample as

where ε_ijk denotes the error (or unexplained) amount, where

and γ_k is a random effect corresponding to the subjects/participants. All the interaction terms, i.e. (αγ)_ik, (αβ)_jk, and (αβγ)_ijk, are also random effects; together they make up the error components of our model.

As before we have the sample version

where e_ijk is the counterpart to ε_ijk in the sample. The null hypotheses for main effects are:

H₀: µ₁_. = µ₂_. = ··· µ_a.(Factor A)

H₀: µ_.₁ = µ_.₂ = ··· µ_.b(Factor B)

These are equivalent to:

H₀: α_i = 0 for all i (Factor A)

H₀: β_j = 0 for all j (Factor B)

In addition, there is a null hypothesis for the effects due to the interaction between factors A and B.

H₀: δ_ij = 0 for all i, j

Definition 2: Using the terminology from Definition 1 of Two Factor ANOVA with Replication, except that we use a for the number of levels in factor A (instead of r) and b for the number of levels in factor B (instead of c), and also adding C = the participant factor and m = number of participants, define:

We can also define four types of between-group terms.

And similarly for BetAC and BetBC. There is also the following BetABC version:

Properties

Property 1:

Proof: It is clear that

If we square both sides of the equation, sum over i, j, and k and then simplify (with various terms equal to zero as in the proof of Property 2 of Basic Concepts of ANOVA), we get the first result. The second result is trivial.

Property 2: If a sample is made as described in Definition 1 of Basic Concepts of ANOVA, with the x_ijk independently and normally distributed and with all $\sigma^2_{.j}$ (or $\sigma^2_{i.}$ ) equal, then

Proof: The proof is similar to that of Property 1 of Basic Concepts of ANOVA.

Theorem 1: Suppose a sample is made as described in Definitions 1 and 2 of Two Factor ANOVA with Replication, with the x_ijkindependently and normally distributed.

If all μ_i are equal and all $\sigma^2_{i}$ are equal then