Repeated Measures ANOVA Post-Hoc Testing

Basic Concepts

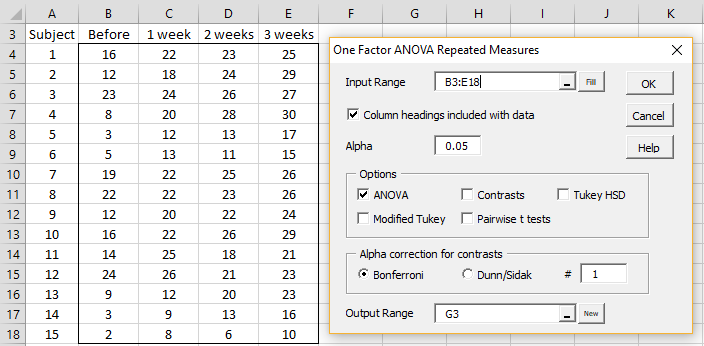
We now show how to use the One Repeated Measures Anova data analysis tool to perform follow-up testing after a significant result on the omnibus repeated-measures ANOVA test. We will use the data for Example 1 of Repeated Measures ANOVA Tool as repeated on the left side of Figure 1.  The right side of Figure 1 shows the dialog box for the One Repeated Measures Anova data analysis tool. 

Figure 1 – Data and dialog box for Repeated Measures Anova

You can access the dialog box as described in Repeated Measures ANOVA Tool. In particular, you need to check one or more of the post-hoc options shown in the dialog box.

Contrasts

Contrast post-hoc tests can be performed as described in Planned Comparisons using the dialog box shown in Figure 1. You only need to select the Contrasts option. You can leave the ANOVA option checked, but this is not required.

The number of contrast tests and the familywise correction (Bonferroni or Dunn/Sidàk) are specified in the Alpha correction for contrasts portion of the dialog box. The output is as Figure 3 of One Within Subjects Factor.

Tukey HSD

Real Statistics supports two versions of the Tukey HSD post-hoc test after Repeated Measures ANOVA. In the first version (Tukey HSD option in the dialog box in Figure 1), the standard error used is , while in the second version (Modified Tukey option in Figure 1), pairwise standard errors are used (as for contrasts).

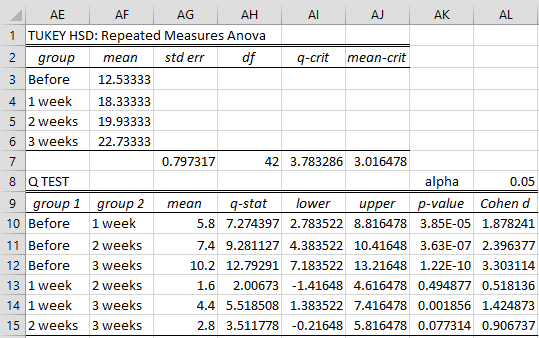
The output for the first version of the Tukey HSD test for the data in Figure 1 is shown in Figure 2.

Figure 2 – Tukey HSD test output

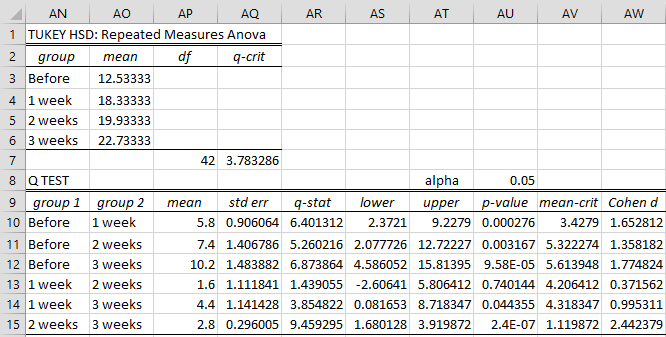
The output for the Modified Tukey HSD test for the data in Figure 1 is shown in Figure 3. This is the preferred version of the test.

Figure 3 – Modified Tukey HSD test output

Here, all but the 1-week vs 2-weeks comparison are significant. Figure 4 displays some formulas used in the output shown in Figure 3.

Cell	Entity	Formula
AP7	df	=dfWF(B4:E18,1)
AQ7	q-crit	=QCRIT(COUNT(AO3:AO6),AP7,AU8,2)
AP10	Difference between means	=ABS(AO3-AO4)
AQ10	s.e. for differences between means	=STDERR(B4:B18-C4:C18)
AR10	q-stat	=AP10/AQ10
AS10	Lower 95% confidence interval	=AP10-AV10
AT10	Upper 95% confidence interval	=AP10+AV10
AU10	p-value	=QDIST(AR10,COUNT(AO$3:AO$6),AP$7)
AV10	Critical value for mean differences	=AQ10*AQ$7
AW10	Cohen’s d	=AR10/SQRT(COUNT(B$4:B$18))

Figure 4 – Key formulas from Figure 3

Note that the formula in cell AQ10 is an array formula.

Pairwise t-tests

Another approach for determining which pairwise groups are significantly different following a significant Repeated Measures ANOVA is to use multiple t-tests followed by one of the following tests to deal with familywise error: Bonferroni, Dunn-Sidàak, Holm’s, Hochberg, Benjamini-Hochberg or Benjamini-Yekutieli. This topic is explored in Multiple Tests.

For Repeated Measures ANOVA, pairwise t-tests refer to pairwise paired sample t-tests.

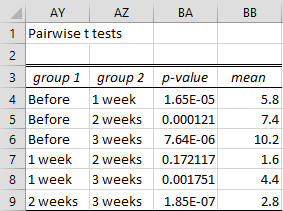
You can obtain pairwise t-tests on the data in Figure 1 using the Pairwise t-tests option in the dialog box in Figure 1. The output is shown in Figure 5.

Figure 5 – Pairwise paired sample t-tests

Here, cell BA4 contains the formula =T.TEST(B4:B18,C4:C18,2,1) and cell BB4 contains the formula =ABS(AVERAGE(B4:B18)-AVERAGE(C4:C18)).

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage

Reference

Howell, D. C. (2010) Statistical methods for psychology (7^th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf