ANCOVA Analysis Tools

ANCOVA Omnibus Test

Example 1: Repeat the analyses of Example 1 of ANOVA Approach to ANCOVA (ANCOVA omnibus test) and Example 1 of Tukey’s HSD for ANCOVA using the Real Statistics ANCOVA data analysis tool.

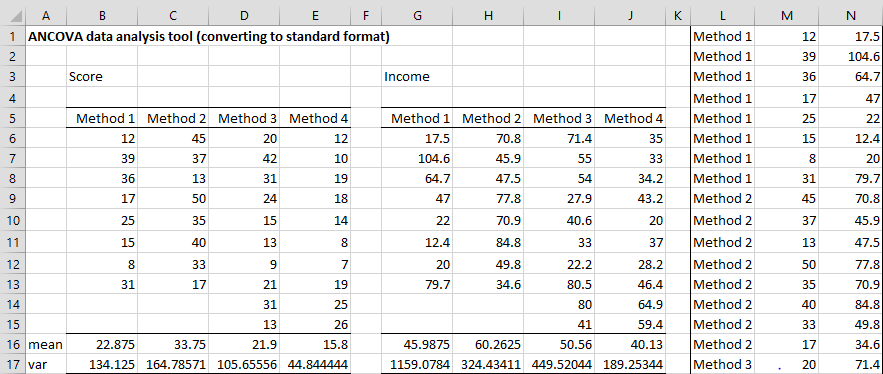
Figure 1 – Input data

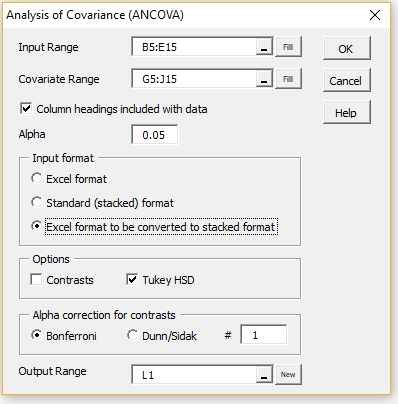
Referring to the input data in Figure 1, press Ctrl-m and double click on the Analysis of Variance option (as shown Figure 1 of ANOVA Analysis Tool) in the main dialog box (or click on the Anova tab in the multipage interface). Select ANCOVA and press OK and fill in the dialog box that appears as shown in Figure 2.

Figure 2 – ANCOVA dialog box

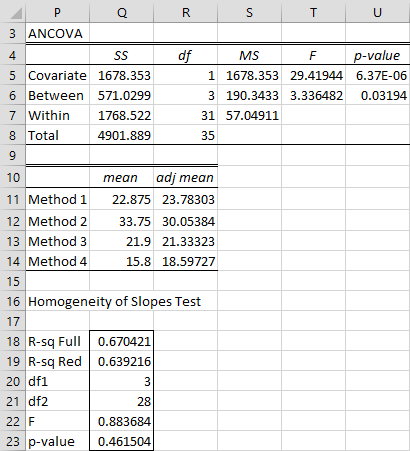
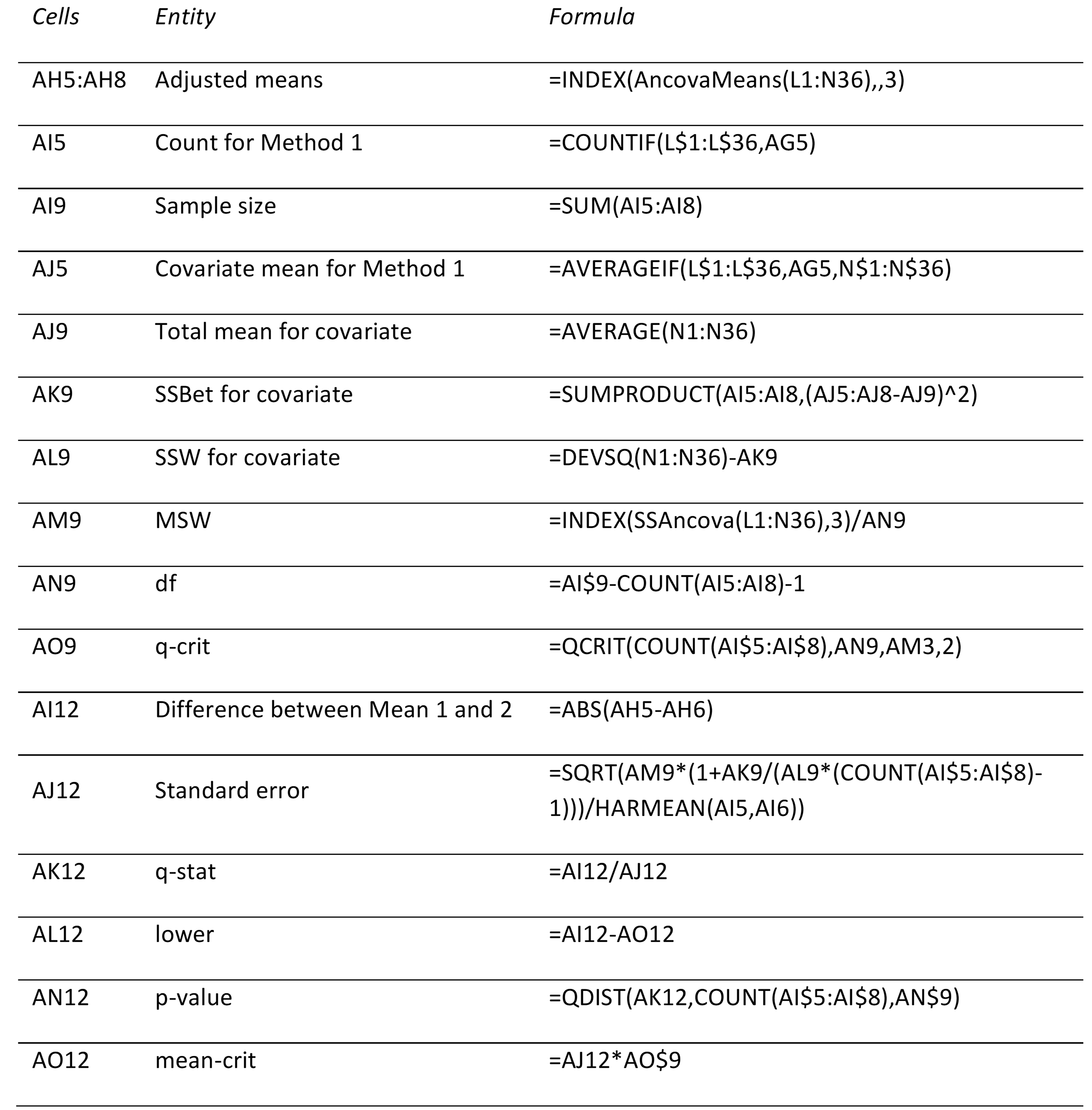
The output consists of the input and covariate data converted to stacked format in range L1:N36, exactly as is shown in Figure 1. This is followed by the ANCOVA report as shown in Figure 3 and the Tukey HSD output shown in Figure 4.

We note that, although the results shown Figure 3 are similar to those displayed in Figure 7 of ANOVA Approach to ANCOVA, there are some differences in the layout. While the output in Figure 7 of ANOVA Approach to ANCOVA reflects the ANOVA approach to ANCOVA, the output in Figure 3 reflects the regression approach to ANOVA (as described in Regression Approach to ANCOVA).

Figure 3 – ANCOVA data analysis output

Whereas the output in Figure 7 of ANOVA Approach to ANCOVA made use only of standard Excel functions, the output in Figure 3 requires use of the following Real Statistics functions.

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack provides the following array functions where R1 is a range, similar to that in L1:N36 of Figure 1, in stacked format.

SSAncova(R1): outputs a column array with SS_Covariate, SS_Bet , SS_W and SS_Tot

AncovaMeans(R1): outputs a k × 3 array with the group names, means and adjusted means for each of the k treatment groups.

AncovaParallel(R1, lab): outputs a 6 × 1 array (or 6 × 2 array including a column of labels if lab = TRUE) with the values: R-square of the model which includes the interaction between the tag variables and the covariate variables, R-square of the model excluding these interactions, as well as df₁ , df₂, F and the p-value of the equal slopes test.

Note that Figure 3 contains the array formula =SSAncova(L1:N36) in range Q5:Q7, the array formula =AncovaMeans(L1:N36) in range P11:R14 and the array formula =AncovaParallel(L1:N36,TRUE) in range P18:Q23.

Note too that the results from the Homogeneity of Slopes Test agree with the results shown in Figure 4 of ANCOVA Assumptions.

Tukey’s HSD and Tukey-Kramer

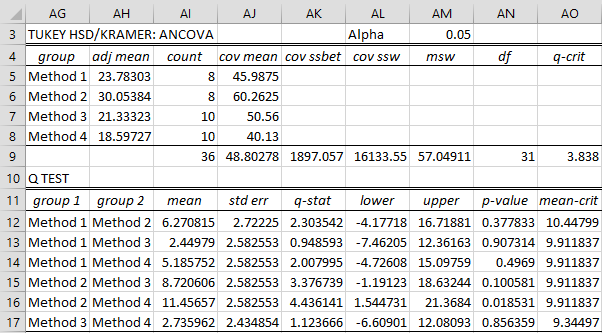
Figure 4 shows the Tukey-Kramer analysis output from the ANCOVA data analysis tool where the contrasts for Method 2 and Method 4 have been filled in. As you can see, the results agree with those shown in Figure 1 of Tukey’s HSD for ANCOVA.

Figure 4 – Tukey HSD/Kramer data analysis

The only pairwise comparison that yields a significant result is Method 2 vs. Method 4.

Key formulas from Figure 4 are shown in Figure 5 (with reference to cells in Figure 1).

Figure 5 – Representative formulas from Figure 4

Contrasts

If we had requested Contrasts analysis, we would have checked this option in the dialog box shown in Figure 2. Alternatively, we can insert the range L1:N36 as the Input Range (leaving the Covariate Range empty), uncheck Column headings included with data and choose the Standard (stacked) format as the Input format as well as the Contrasts option. Since we plan to perform two contrast tests we change the # field in the Alpha correction for contrasts from 1 to 2.

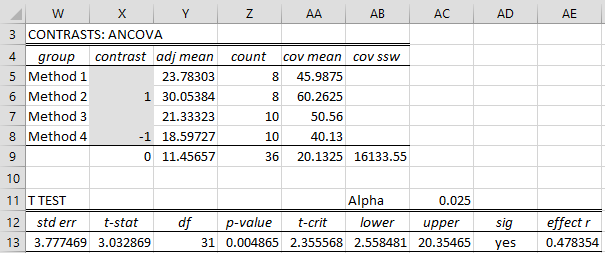
The output is shown in Figure 6 (after filling in the contrast coefficients in range X5:X8).

Figure 6 – Contrast data analysis

The results are similar to those in Figure 1 of Contrasts for ANCOVA. The formulas in Figure 6 are similar to those in Figure 5. The formula in cell X13 is

=SQRT(INDEX(SSAncova(L1:N36),3)/(Z9-COUNTA(W5:W8)-1)* (SUMPRODUCT(X5:X8^2,1/Z5:Z8)+AA9^2/AB9))

Note too that since we plan on making two contrast tests, the alpha value in cell AC11 is .05/2 = .025 using a Bonferroni correction.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Howell, D. C. (2010) Statistical methods for psychology (7^th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf

Schmuller, J. (2009) Statistical analysis with Excel for dummies. Wiley
https://www.wiley.com/en-us/Statistical+Analysis+with+Excel+For+Dummies%2C+3rd+Edition-p-9781118464311